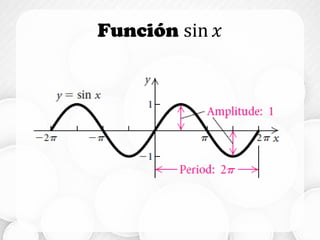
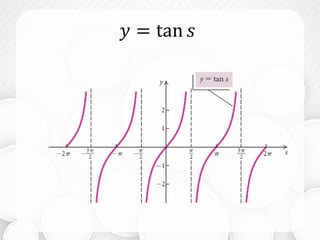
Este documento trata sobre funciones trigonométricas y sus gráficas. Explica las seis funciones básicas (seno, coseno, tangente, cosecante, secante y cotangente), y analiza sus gráficas, dominios, períodos y propiedades como paridad. También incluye ejercicios de práctica para graficar estas funciones usando transformaciones como reflexiones y traslaciones.

1. Funciones circulares:
Gráficas y propiedades
Trigonometría
TR3: Funciones trigonométricas y
sus gráficas

2. 𝜃

3. Funciones circulares básicas
• sin 𝑠 = 𝑦
• cos 𝑠 = 𝑥
• tan 𝑠 =
𝑦
𝑥
(𝑥 ≠ 0)
• csc 𝑠 =
1
𝑦
(𝑦 ≠ 0)
• sec 𝑠 =
1
𝑥
(𝑥 ≠ 0)
• cot 𝑠 =
𝑥
𝑦
(𝑦 ≠ 0)

4. • Halla la reflexión en el eje x para el punto
3
5
,
4
5
.
Reflexiones en el
Círculo Unitario
𝑥² + 𝑦² = 1; −1 ≤ 𝑥 ≤ 1
3
5
2
+ 𝑦² = 1
𝑦² = 1 −
9
25
=
16
25
𝑦 = ±
4
5
3
5
, −
4
5

5. Reflexiones en el
Círculo Unitario
• Dada la coordenada 𝑥 =
1
2
, halla el valor
de la coordenada y en el círculo unitario.
1
2
2
+ 𝑦² = 1
𝑦² = 1 −
1
4
=
3
4
𝑦 =
3
4
=
3
2
1
2
,
3
2

6. Reflexiones en el
Círculo Unitario
• Equivalencias de ángulos

7. Práctica
• Para cada punto localizado en el círculo
unitario, halla la reflexión en el los ejes x y
y, como también la reflexión en el origen.

8. Solución

9. Solución

10. Solución

11. Solución

12. Halla el valor de cada función

13. Solución a.

14. Solución b.

15. Solución c.

16. Solución d.

17. Solución e.
No está definida.

18. Solución f.

19. Graficando las funciones de
Seno y Coseno

20. Graficando las funciones de
Seno y Coseno

22. Tablas de Valores

24. Gráfica de la función Seno

25. Gráfica de la función Coseno

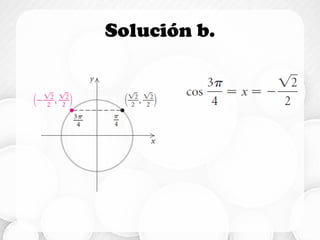
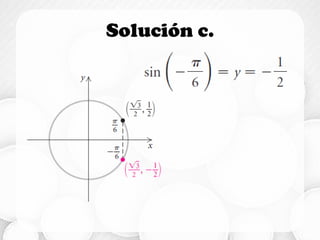
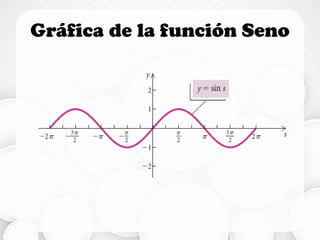
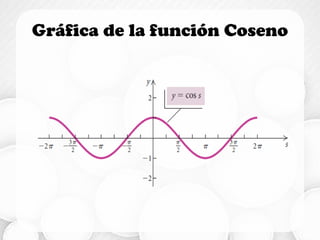
26. Dominio y Rango
• Dominio: −∞, ∞
• Rango: [−1,1]

27. Función periódica
• Gráfica periódica: Gráfica que muestra un
patrón repetitivo.
• Una función f se dice periódica, si existe
una constante positiva p tal que:
𝑓 𝑠 + 𝑝 = 𝑓 𝑠
para todo s en el dominio de f.
• El valor positivo p menor es llamado el
periodo de la función.

28. Función períodica

29. Identidades
• sin 𝑠 + 𝑘 2𝜋 = sin 𝑠
• cos 𝑠 + 𝑘 2𝜋 = cos 𝑠

30. Amplitud
• La amplitud de una función periódica es
definida como la mitad de la distancia
entre el valor máximo y el mínimo.
• Siempre es positiva.

31. Función sin 𝑥

32. Función cos 𝑥

33. Paridad
• Función seno es una función impar:
sin −𝑠 = − sin 𝑠
• Las coordenadas son de signos opuestos.

34. Paridad
• Función coseno es una función par:
cos −𝑠 = cos 𝑠
• Las coordenadas son del mismo signo.

35. Graficando funciones
• tan 𝑠 =
𝑦
𝑥
=
sin 𝑠
cos 𝑠

36. Tan s
• La función Tan s no está definida para los
puntos donde el cos 𝑠 = 0.
• En esos puntos la función tiene asíntotas
verticales.

37. Tan s
• Notamos que…

38. 𝑦 = tan 𝑠

39. 𝑦 = cot 𝑠

40. 𝑦 = csc 𝑠

41. 𝑦 = sec 𝑠

42. Ejercicios de práctica
• Dadas las siguientes coordenadas, halla
las reflexiones en:
(a) eje x, (b) eje y, (c) origen

43. • Halla el valor exacto de cada función
haciendo uso de las coordenadas
correspondientes en el círculo unitario.
1) sin 𝜋 2) cos − 𝜋
3
3) cot 7𝜋
6
4) tan 11𝜋
4 5) sin(−3𝜋) 6) csc 3𝜋
4
7) cos 5𝜋
6 8) tan − 𝜋
4 9) sec 𝜋
2
10) cos 10𝜋 11) cos 𝜋
6 12) sin(−5𝜋)

44. Gráfica #1
• Grafica la función de 𝑦 = sin 𝑥.
– Utiliza la reflexión para graficar 𝑦 = sin(−𝑥).
– Utiliza la reflexión para graficar 𝑦 = − sin 𝑥.
– Compara las gráficas.

45. Gráfica #2
• Grafica la función de 𝑦 = cos 𝑥.
– Utiliza la reflexión para graficar 𝑦 = cos(−𝑥).
– Utiliza la reflexión para graficar 𝑦 = − cos 𝑥.
– Compara las gráficas.

46. Gráfica #3
• Grafica la función de 𝑦 = sin 𝑥.
– Utiliza la traslación para graficar
𝑦 = sin(𝑥 + 𝜋).
– Utiliza la reflexión para graficar 𝑦 = − sin 𝑥.
– Compara las gráficas.

47. Gráfica #4
• Grafica la función de 𝑦 = sin 𝑥.
– Utiliza la traslación para graficar
𝑦 = sin(𝑥 − 𝜋).
– Utiliza la reflexión para graficar 𝑦 = − sin 𝑥.
– Compara las gráficas.

48. Gráfica #5
• Grafica la función de 𝑦 = cos 𝑥.
– Utiliza la traslación para graficar
𝑦 = cos(𝑥 + 𝜋).
– Utiliza la reflexión para graficar 𝑦 = − cos 𝑥.
– Compara las gráficas.

49. Gráfica #6
• Grafica la función de 𝑦 = cos 𝑥.
– Utiliza la traslación para graficar
𝑦 = cos(𝑥 − 𝜋).
– Utiliza la reflexión para graficar 𝑦 = − cos 𝑥.
– Compara las gráficas.

50. Contesta
1. ¿Cuáles de las seis funciones
trigonométricas son impares?
¿Cuáles son pares?
Funciones pares: coseno y secante.
Funciones impares: seno, cosecante, tangente
y cotangente.

51. Contesta
2. ¿Cuáles de las seis funciones
trigonométricas tienen periodos iguales a
𝜋?
¿Cuáles tienen periodos iguales a 2𝜋?
Periodo igual a 𝜋: secante, cosecante, tangente
y cotangente.
Periodo igual a 2𝜋: seno y coseno.

52. Determina el dominio de las
siguientes funciones
1. 𝑓 𝑥 = cos 𝑥 2. 𝑔 𝑥 =
1
sin 𝑥
3. 𝑓 𝑥 =
sin 𝑥
cos 𝑥
4. 𝑔 𝑥 = log(sin 𝑥)
Signos de las funciones trigonométricas
según el cuadrante
Función I II III IV
sin 𝑥 + + - -
cos 𝑥 + - - +
tan 𝑥 + - + -
0, 𝜋
2 ∪ 3𝜋
2 ,2𝜋 (0, 𝜋) ∪ (𝜋, 2𝜋)
0, ൯𝜋
2
∪ ቀ 𝜋
2
, ቁ
3𝜋
2
∪ ቀ3𝜋
2
, 2𝜋
0, 𝜋

53. Parea cada gráfica con su
función correspondiente
1) 𝑦 = cos 2𝑥 2) 𝑦 = 1
2 sin 𝑥 + 1
3) 𝑦 = −2 sin 1
2 𝑥 − 3 4) 𝑦 = − cos 𝑥 − 𝜋
2
𝑑 𝑎
𝑐 𝑏