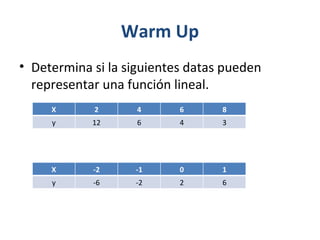
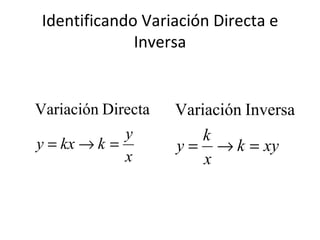
Este documento presenta los conceptos de variación directa, conjunta, inversa y combinada en matemáticas. Explica cada tipo de variación a través de ecuaciones y ejemplos, y proporciona problemas para que los estudiantes practiquen identificar y resolver diferentes situaciones de variación.

1. Sección 8 – 1 Funciones de Variación Matemática Avanzada Undécimo Grado

2. Warm Up Resuelve cada ecuación.

3. Warm Up Determina si la siguientes datas pueden representar una función lineal. X 2 4 6 8 y 12 6 4 3 X -2 -1 0 1 y -6 -2 2 6

4. Objetivos Resolver problemas que envuelvan variación directa, conjunta, inversa y combinada.

5. Variación Directa Una variación directa es una relación entre dos variables x y y que puede ser escrita de la forma y = kx , donde k ≠ 0. En esta relación, k es la constante de variación . Para la ecuación y = kx , y varía directamente con x .

6. Escribiendo y Graficando Variación Directa Dado que y varía directamente con x y cuando x = 3.5, y = 14. Escribe y grafica la función de variación directa. Dado que y varía directamente con x y cuando x = 6, y = 27. Escribe y grafica la función de variación directa.

7. Resolviendo Problemas de Variación Directa La circunferencia de un círculo C varía directamente con el radio r y C = 7π pies cuando r = 3.5 pies. Encuentra r cuando C = 4.5π pies. El costo de un artículo en euros e varia directamente con el costo del artículo en dólares d , e = 3.85 euros cuando d = $5.00. Encuentra d cuando e = 10.00 euros.

8. Variación Conjunta Una variación conjunta es una relación entre tres variable que puede ser escrita de la forma y = kxz , donde k es la constante de variación. Para la ecuación y = kxz , y varía conjuntamente con x y z .

9. Resolviendo Problemas de Variación Conjunta El área A de un triángulo varía conjuntamente con la base b y la altura h , y A = 12m 2 cuando b = 6m y h = 4m. Encuentra b cuando A = 36m 2 y h = 8m. El volumen V de un cono varía conjuntamente con el área de la base B y la altura h , y V = 12π pies 3 cuando B = 9π pies 2 y h = 4 pies. Encuentra B cuando V = 24π pies 3 y h = 9 pies.

10. Variación Inversa Una variación inversa es una relación entre dos variables x y y que puede ser escrita de la forma y = k/x , donde k ≠ 0. Para la ecuación y = k/x , y varía inversamente con x .

11. Escribiendo y Graficando Variación Inversa Dado que y varía inversamente con x , y y = 3 cuando x = 8. Escribe y grafica la función de variación inversa. Dado que y varía inversamente con x , y y = 4 cuando x = 5. Escribe y grafica la función de variación inversa.

12. Aplicaciones El tiempo t que le toma a un grupo de voluntarios construir una casa varía inversamente con el número de voluntarios v. Si 20 voluntarios pueden construir una casa en 62.5 horas, ¿cuántos voluntarios se necesitarán para construir una casa en 50 horas?

13. Aplicaciones El tiempo necesario para completar cierta carrera varía inversamente con la velocidad s promedio del corredor. Si un corredor con una velocidad promedio de 8.82 mi/h completa la carrera en 2.97 h, ¿cuál es la velocidad promedio de un corredor que completa la carrera en 3.5 h?

14. Identificando Variación Directa e Inversa

15. Identificando Variación Directa e Inversa Determina si la siguiente conjuntos de data representan variación directa, inversa o ninguna. X 3 8 9 y 9 24 27 X 4.5 12 2 y 8 3 18 X 6.5 13 104 y 8 4 0.5 X 3 6 8 y 5 14 21

16. Variación Combinada Una variación combinada es una relación que contiene variación directa e inversa. Las cantidades que varían directamente aparecen en el numerador y las que varían inversamente aparecen en el denominador.

17. Aplicación a Química El volumen V de un gas varia inversamente con la presión P y directamente con la temperatura T . Cierto gas tiene un volumen de 10 litros (L), una temperatura de 300 kelvins (K) y una presión de 1.5 atmósferas (atm). Si el gas está comprimido a un volumen de 7.5 L y es calentado a una temperatura de 350 K, ¿cuál sería la nueva presión?

18. Aplicación a Física El cambio en temperatura T de un cable de aluminio varía inversamente con su masa m y directamente con la cantidad de energía calórica E transferida. La temperatura de un cable de aluminio con una masa de 0.1 kg aumenta a 5°C cuando se le aplican 450 julios (J) de energía calórica. ¿Cuánta energía calórica debe ser transferida a un cable de aluminio con una masa de 0.2 kg para aumentar su temperatura a 20°C?

19. Asignación Página 574 Ejercicios 17 – 20, 22, 24 – 26, 28 – 31