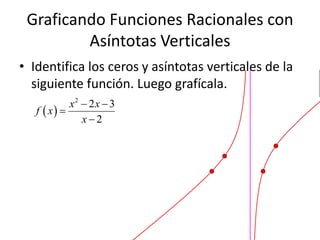
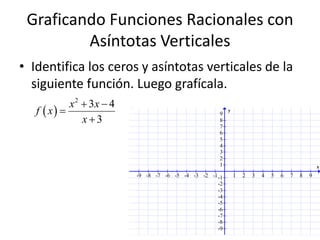
Este documento describe diferentes tipos de variación, incluyendo variación directa, variación inversa, variación conjunta y variación combinada. También describe expresiones racionales y funciones racionales, incluyendo cómo graficarlas y resolver ecuaciones racionales.

1. Tema VIII
Funciones Racionales
Precálculo

2. Variación Directa
• Una variación directa es una relación entre
dos variables x y y que puede ser escrita de la
forma y = kx, donde k ≠ 0.
• En esta relación, k es la constante de
variación.
• Para la ecuación y = kx, y varía directamente
con x.

3. Escribiendo y Graficando Variación
Directa
• Dado que y varía directamente con x y cuando
x = 3.5, y = 14. Escribe y grafica la función de
variación directa.
• Dado que y varía directamente con x y cuando
x = 6, y = 27. Escribe y grafica la función de
variación directa.

4. Resolviendo Problemas de Variación
Directa
• La circunferencia de un círculo C varía
directamente con el radio r y C = 7π pies
cuando r = 3.5 pies. Encuentra r cuando C =
4.5π pies.
• El costo de un artículo en euros e varia
directamente con el costo del artículo en
dólares d, e = 3.85 euros cuando d = $5.00.
Encuentra d cuando e = 10.00 euros.

5. Variación Conjunta
• Una variación conjunta es una relación entre
tres variable que puede ser escrita de la forma
y = kxz, donde k es la constante de variación.
• Para la ecuación y = kxz, y varía
conjuntamente con x y z.

6. Resolviendo Problemas de Variación
Conjunta
• El área A de un triángulo varía conjuntamente
con la base b y la altura h, y A = 12m2 cuando
b = 6m y h = 4m. Encuentra b cuando A =
36m2 y h = 8m.
• El volumen V de un cono varía conjuntamente
con el área de la base B y la altura h, y V = 12π
pies3 cuando B = 9π pies2 y h = 4 pies.
Encuentra B cuando V = 24π pies3 y h = 9 pies.

7. Variación Inversa
• Una variación inversa es una relación entre
dos variables x y y que puede ser escrita de la
forma y =k/x, donde k ≠ 0.
• Para la ecuación y =k/x, y varía inversamente
con x.

8. Escribiendo y Graficando Variación
Inversa
• Dado que y varía inversamente con x, y y = 3
cuando x = 8. Escribe y grafica la función de
variación inversa.
• Dado que y varía inversamente con x, y y = 4
cuando x = 5. Escribe y grafica la función de
variación inversa.

9. Aplicaciones
• El tiempo t que le toma a un grupo de
voluntarios construir una casa varía
inversamente con el número de voluntarios v.
Si 20 voluntarios pueden construir una casa en
62.5 horas, ¿cuántos voluntarios se
necesitarán para construir una casa en 50
horas?

10. Aplicaciones
• El tiempo necesario para completar cierta
carrera varía inversamente con la velocidad s
promedio del corredor. Si un corredor con una
velocidad promedio de 8.82 mi/h completa la
carrera en 2.97 h, ¿cuál es la velocidad
promedio de un corredor que completa la
carrera en 3.5 h?

11. Variación Combinada
• Una variación combinada es una relación que
contiene variación directa e inversa.
• Las cantidades que varían directamente
aparecen en el numerador y las que varían
inversamente aparecen en el denominador.

12. Aplicación a Química
• El volumen V de un gas varia inversamente
con la presión P y directamente con la
temperatura T. Cierto gas tiene un volumen de
10 litros (L), una temperatura de 300 kelvins
(K) y una presión de 1.5 atmósferas (atm). Si el
gas está comprimido a un volumen de 7.5 L y
es calentado a una temperatura de 350 K,
¿cuál sería la nueva presión?

13. Aplicación a Física
• El cambio en temperatura T de un cable de
aluminio varía inversamente con su masa m y
directamente con la cantidad de energía
calórica E transferida. La temperatura de un
cable de aluminio con una masa de 0.1 kg
aumenta a 5°C cuando se le aplican 450 julios
(J) de energía calórica. ¿Cuánta energía
calórica debe ser transferida a un cable de
aluminio con una masa de 0.2 kg para
aumentar su temperatura a 20°C?

14. Expresiones Racionales
• Una expresión racional es un cociente de dos
polinomios.
• Ejemplos:
x 4
2
10 x3
x2 x 6
2
x7

15. Simplificando Expresiones Racionales
• Simplifica. Identifica cualquier valor de x para
los cuales la función esté indefinida.
3x 7
x2  2 x  3
1. 2. 2
2 x4 x  5x  4
10 x8 x2  x  2
3. 4. 2
6x4 x  2x  3

16. Simplificando Factorizando -1
• Simplifica. Identifica cualquier valor de x para
los cuales la función esté indefinida.
2x  x2
1. 2
x x2
4x  x 2
2. 2
x  2x  8

17. Multiplicando Expresiones Racionales
1. Factoriza completamente el numerador y el
denominador.
2. Divide los factores en común del
denominador y el numerador.
3. Multiplica los numeradores. Luego multiplica
los denominadores.
4. Asegúrate que el numerador y el
denominador no tengan factores en común
diferentes de 1.

18. Multiplicando Expresiones Racionales
• Multiplica. Asume que todas las expresiones
están definidas.
4 5
2 x y 15 x 2 x2 x4
1.  3 2 2.  2
3x 2
8x y 3x  12 x  4
3x5 y 3 10 x3 y 4 x 3 x 5
3.  2 5 4.  2
3 7
2x y 9x y 4 x  20 x  9

19. Dividiendo Expresiones Racionales
• Divide. Asume que todas las expresiones están
definidas.
3
4x 16 x5  4 x3 x5  x 4  2 x3
1.  5 2. 2 
2
9x y 9 y x x2 x2 1
5x4 15 x4  9 x2 x 4  2 x3  8 x 2
3. 2 2  5 4. 2 
8x y 8 y x  4x  3 x 2  16

20. Resolviendo Ecuaciones Racionales
Simples
• Resuelve. Coteja tu solución.
x 9
2
x 2  3x  4
7 5
x3 x 1
x 2  3x  10
x 2  25 7
 14 x2
x 5

21. Sumando y Restando Expresiones
Racionales
• Suma o resta. Identifica los valores para los
cuales la expresión no está definida.
3x  4 2 x  5 2 x 1 1
1)   
x3 x3 6) x 4
x 1 8) x 2 x
x 1 x  4 x4
2) 
x3 x2 x x2
x 1 x x 1
3)  x2 1
x  3x  2 x  1
2
7)
x
2 x 2  16 x  4
4)  x 1
x 4
2
x2

22. Funciones Racionales
• Una función racional 1
Su "parent function" es f  x   .
es una función cuya x
regla puede ser
escrita como una
Asíntota vertical
razón de dos x=0
polinomios.
• Su gráfica se conoce
Asíntota horizontal
como una hipérbola y=0

23. Funciones Racionales
• Una función discontinua es una función cuya
gráfica tiene uno o más saltos, interrupciones
u hoyos.
– Ej. Funciones racionales
• Una función continua es una función cuya
gráfica es una línea recta o curva continua, sin
espacios ni interrupciones.
– Ej. Funciones lineales, cuadráticas, polinomiales,
exponenciales, etc.

24. Ceros y Asíntotas Verticales
p  x
Si f  x   , donde p y q son funciones polinomiales en forma estándar
q  x
sin factores en común, diferente de 1, entonces la función f tiene:
 ceros en cada valor real de x para el cual p  x   0.
 una asíntota vertical en cada valor real de x para el cual q  x   0.

25. Graficando Funciones Racionales con
Asíntotas Verticales
• Identifica los ceros y asíntotas verticales de la y
siguiente función. Luego grafícala. 9
8
x2  2 x  3 7
f  x  6
x2 5
4
3
2
1
-9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-1
-2
-3
-4
-5
-6

26. Graficando Funciones Racionales con
Asíntotas Verticales
• Identifica los ceros y asíntotas verticales de la y S
siguiente función. Luego grafícala. 9 x
f
8
x2  7 x  6 7
f  x  6
x3 5
4
3
2
1
-9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7
-1
-2
-3
-4
-5
-6

27. Graficando Funciones Racionales con
Asíntotas Verticales
• Identifica los ceros y asíntotas verticales de la
siguiente función. Luego grafícala.
x 2  3x  4
f  x  y
x3
9
8
7
6
5
4
3
2
1 x
-9 -8 -7 -6 -5 -4 -3 -2 -1 -1 1 2 3 4 5 6 7 8 9
-2
-3
-4
-5
-6
-7
-8
-9

28. Asíntotas Horizontales
p  x
Sea f  x   , donde p y q son funciones polinomiales en forma
q  x
estándar sin factores en común, diferente de 1. La gráfica de f tiene,
como máximo, una asíntota horizontal.
 Si el grado de p  grado de q, no hay asíntota horizontal.
 Si el grado de p  grado de q, la asíntota horizontal es la recta y  0.
 Si el grado de p  grado de q, la asíntota horizontal está dada por la
coeficiente lider de p
recta y  .
coeficiente lider de q

29. Graficando Funciones Racionales con
Asíntotas Verticales y Horizontales
• Identifica los ceros y asíntotas de cada
función. Luego grafica.
x2  x  6
f  x 
x

30. Graficando Funciones Racionales con
Asíntotas Verticales y Horizontales
• Identifica los ceros y asíntotas de cada
función. Luego grafica.
x 1
f  x  2
x

31. Graficando Funciones Racionales con
Asíntotas Verticales y Horizontales
• Identifica los ceros y asíntotas de cada
función. Luego grafica.
2x2  2
f  x  2
x 4

32. Graficando Funciones Racionales con
Asíntotas Verticales y Horizontales
• Identifica los ceros y asíntotas de cada
función. Luego grafica.
x 2  3x  4
f  x 
x

33. Graficando Funciones Racionales con
Asíntotas Verticales y Horizontales
• Identifica los ceros y asíntotas de cada
función. Luego grafica.
x2
f  x  2
x 1

34. Graficando Funciones Racionales con
Asíntotas Verticales y Horizontales
• Identifica los ceros y asíntotas de cada
función. Luego grafica.
4 x  12
f  x 
x 1

35. Ecuación Racional
• Una ecuación racional es una ecuación que
contiene una o más expresiones racionales.

36. Resolviendo Ecuaciones Racionales
8
Resuelve la ecuación x   6
x

37. Resolviendo Ecuaciones Racionales
10 4
Resuelve la ecuación  2
3 x

38. Resolviendo Ecuaciones Racionales
6 5 7
Resuelve la ecuación   
x 4 4

39. Resolviendo Ecuaciones Racionales
18
Resuelve la ecuación x   3
x

40. Resolviendo Ecuaciones Racionales
• Resuelve cada ecuación.
3x 2x  3 5x 3x  4
 
x 3 x 3 x2 x2
2x  9 x 5
  2x  5 x 11
x7 2 x7  
x 8 2 x 8