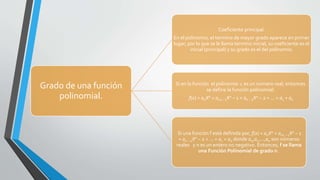
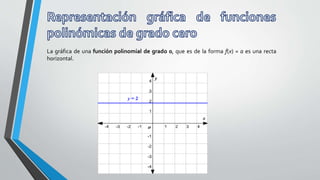
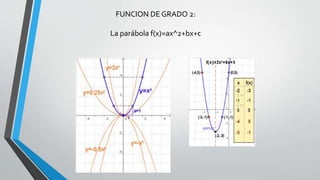
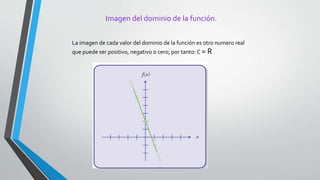
El documento presenta información sobre funciones polinomiales de grado cero, uno y dos. Explica que las funciones constante, lineal y cuadrática son casos especiales de funciones polinomiales. Describe las características de cada grado, incluyendo sus expresiones, representaciones gráficas y parámetros.

1. COLEGIO DE BACHILLERES DETABASCO
PLANTEL 34
INTEGRANTES:
Domínguez Carrillo Jacqueline
Domínguez Hernández Mary Carmen
Flores Sánchez Daniel
Gómez Díaz María José
Gómez Márquez Karely del Carmen
Fecha de entrega: 29 de Febrero de 2016
BLOQUE 3. EMPLEAS FUNCIONES POLINOMIALES DE
GRADO CERO, UNO Y DOS.
Docente: Ing.Ángel Córdova Domínguez

2. Bloque 3.- Empleas
funciones polinomiales de
grado cero, uno y dos.
 Modo general de las funciones polinomiales.
 Forma polinomial de funciones de grado cero, uno y dos.
 Representación grafica de funciones de grado cero, uno y
dos.
 Características de las funciones polinomiales de grado
cero, uno y dos.
 Parámetros de las funciones de grado cero, uno y dos.
Matemáticas IV.
Ing. Ángel Córdova Domínguez

3. 3.1Modelo general de las funciones polinomiales.
f(x)=anxn+an-1xn-1+…+a1x1+a0x0.
Polinomio de grado “n”
Con a0,a1,a2,…,an-1,an € R
Y an ≠ 0
x0 = 1; entonces a0 es el termino independiente
Ejemplo: (grado de los polinomios)
• X2+2x1+1
• 7x4+3x-9
• X+1
• 8

4. Forma Polinomial de
Funciones de Grado Cero, Uno
y Dos.

5. ¿Qué es un
polinomio?
Se denomina
polinomio a la suma
de varios monomios.
Es una expresión
hecha con constantes
variables y
exponentes.
Están combinados
usando sumas, restas
y multiplicaciones.

6. Grado de una función
polinomial.
Coeficiente principal.
En el polinomio, el termino de mayor grado aparece en primer
lugar; por lo que se le llama termino inicial, su coeficiente es el
inicial (principal) y su grado es el del polinomio.
Si en la función el polinomio x es un numero real, entonces
se define la función polinomial:
f(x) = anXn + an1 − 1Xn − 1 + an − 2Xn − 2 + ... + a1 + a0
Si una función f está definida por, f(x) = anXn + an1 − 1Xn − 1
+ an − 2Xn − 2 + ... + a1 + a0 donde a0,a1,...,an son números
reales y n es un entero no negativo. Entonces, f se llama
una Función Polinomial de grado n.

7. El grado de un termino es el del exponente de x en dicho
termino, y el grado de toda la expresión es igual al del termino de
mayor grado.
f (x) = 0 se llama función polinomial cero para distinguirla de
f (x) = ao donde ,que es una función polinomial de grado cero y
corresponde a la funcion constante.
Si n=1, la expresión queda de la siguiente
forma:
f (x) = a1x + a0 = mx + b
Que es la forma general de la función
lineal; y si n=2 entonces:
f (x) = a2x2 + a1x +a0 = ax2 +bx +c
Que corresponde a la forma general de la
función cuadrática.
Por lo anterior se deduce que
las funciones constante,
lineal y cuadrática son casos
especiales de la función
polinomial.
Cuando f (x) = 0 se
tiene una ecuación
polinomial de grado n.
Un valor de x que satisface la
ecuación recibe el nombre de
raíz o solución de la
ecuación, también se dice
que es un cero del polinomio.

8. EJEMPLOS

10. Representación Grafica de
Funciones de Grados Cero,
Uno y Dos

11. Grado Nombre Expresión
0 función constante y = a
1 función lineal y = ax + b es un binomio del primer
grado
2 función cuadrática y = ax² + bx + c es un trinomio del
segundo grado
3 función cúbica y = ax³ + bx² + cx + d es un
cuatrinomio de tercer grado
Algunas funciones polinómicas reciben un nombre especial según el grado del
polinomio:

12. La gráfica de una función polinomial de grado 0, que es de la forma f(x) = a es una recta
horizontal.

13. La forma de esta función de grado uno es la ecuación de la línea recta, que tiene su gráfica como aparece de
forma oblicua.
y = m x + b

14. Las funciones polinómicas de grado 2 son del tipo , con . Sus
representaciones gráficas son las famosas parábolas. Hay dos posibles representaciones que
dependen del signo de

15. CARACTERISTICAS DE LAS
FUNCIONES
POLINOMIALES DE
GRADOS CERO,UNOY
DOS

16. FUNCIONES DE GRADO CERO :
La fórmula de la función de grado 0 es la siguiente: F(x)= a
por ejemplo:
F(x)=7. Es de grado cero, se le conoce como función constante.

17. En el caso de las funciones polinómicas f(0) coincide con el
coeficiente de grado cero o término independiente de la
función, por tanto nada más ver la expresión ya reconocemos
un punto de su gráfica, el corte en el eje de ordenadas
La grafica de f(x)=ax+3 corta en (3,0)
FUNCION DE GRADO 1:

18. FUNCION DE GRADO 2:
La parábola f(x)=ax^2+bx+c

19. 3.5 parámetros de las funciones de
grados ,cero, uno y dos.
Grafica y parámetros
La expresión algebraica de esta función es de la f(x)=mx
+ b donde los parámetros m y b corresponden
respectivamente a su pendiente y a su ordenada al
origen.
Grafica de la función lineal
Es el conjunto del plano que corresponde a los pares
ordenados de la función :
f(x)=2x + 1, x E R
Dominio y rango
La función lineal tienen como dominio y
rango a los números reales.
Sea f: f(x)=2x + 1

20. Representación geométrica de la gráfica
de la función lineal.
Si en el plano se localizan los
puntos a estos y se unen
consecutivamente ,se obtiene
la representación geométrica
de una parte de la gráfica.

21. La imagen de cada valor del dominio de la función es otro numero real que puede ser
positivo ,negativo o cero ,por ello ,la imagen del dominio de la función lineal es:
Grafica de la función lineal.

22. Propiedades de la función lineal.
a) Inyectividad
Existen dos números reales diferentes, tales
que las imágenes que les corresponden también
son diferentes ,
la función lineal es inyectiva.
Si cualquier recta horizontal interseca a la
grafica de f(x) en, a lo mas, un punto ,entonces
f(x) es inyectiva, y si interseca a la grafica de f(x)
en mas de un punto entonces f(x) no es
inyectiva.
b) Suprayectividad
La imagen de la función lineal es igual al
contrario=C=R ;por lo tanto, la función lineal
es supreyectiva
c) Biyectividad
La función lineal es inyectiva y
suprayectiva,entonces también es biyectiva
• Las funciones constante, identidad y lineal se
representan en forma geométrica por medio de
una línea recta ;por ello ,comúnmente se les
llama funciones lineales.
En general ,una función lineal real de la forma
f(x)=mx + b donde m,b,x son números reales,
de los cuales m y b son constantes.

23. Grafica de la función.
Es el conjunto de los puntos del plano que representan a
los pares ordenados de la función :
f(x)=3x + 2 E R
Representación geométrica de la grafica de la
función.
• Así se puede obtener los valores de
y o f(x).

24. Imagen del dominio de la función.
La imagen de cada valor del dominio de la función es otro numero real
que puede ser positivo, negativo o cero; por tanto: C = R

25. Propiedades de la función.
a) Inyectividad
Es inyectiva porque dada dos números reales diferentes, sus respectivas imágenes también son
diferentes. Si se trazan rectas paralelas al eje x se observa que intersecan la representación de f
en, a lo mas ,un punto.
b) Suprayectividad
Es supreyectiva porque su imagen es igual al contradominio B= C= R
C) Biyectividad
La función es inyectiva y suprayectiva,por tanto, también es biyectiva.

26. Representación grafica de la función.
• En general ,la ecuación lineal y = mx + b se puede expresar como una
función lineal :
f(x)=mx + b
La diferencia entre una ecuación lineal y una función lineal es:
Una ecuación lineal es una igualdad que contiene uno o mas números
indeterminados .
Una función lineal es una regla de correspondencia que asocia a cada
elemento de un conjunto con uno y solo un elemento de otro conjunto.
En la ecuación x + 3 = 7 se establece la condición de que si a x se le suma
3 se obtiene como resultado 7 y, en consecuencia x=4.
En cambio en una función podemos elegir cualquier valor dentro de su
dominio y determinar el que le corresponde en el contradominio .Asi,en
la función f(x)=x + 3,la regla de correspondencia establece que para
cualquier valor de x dentro de su dominio al sumarle 3 se obtiene su
asociado en el contradominio.
• La representación grafica de una
función lineal nos permite identificar,
según el trazo, algunas de sus
características y propiedades.