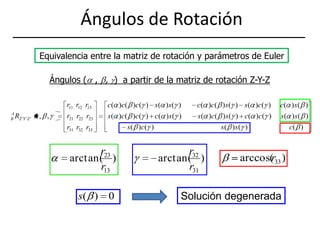
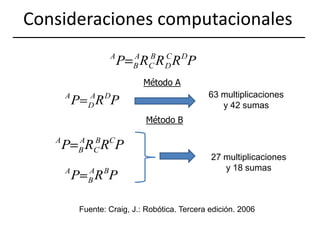
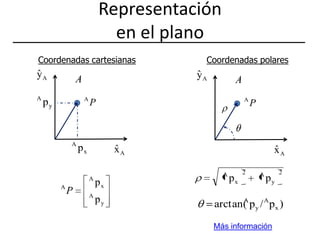
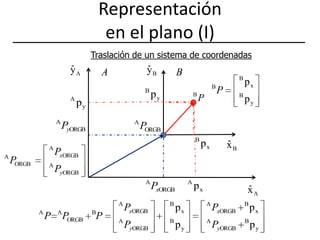
Este documento describe diferentes representaciones de la posición y orientación en el plano y el espacio, incluyendo coordenadas cartesianas, polares, cilíndricas y esféricas. También explica cómo representar traslaciones, rotaciones y combinaciones de ambas mediante matrices de transformación homogénea, y cómo aplicar estos conceptos a robótica móvil y brazos articulados. Finalmente, analiza ángulos de Euler y RPY para representar orientaciones y sus equivalencias con matrices de rotación.

1. Fundamentos de la posición y orientación

2. Representación en el planoCoordenadas cartesianasCoordenadas polaresMás información

3. Representación en el plano (I)Traslación de un sistema de coordenadas

4. Representación en el plano (II)Rotación de un sistema de coordenadas

5. Representación en el plano (III)Rotación y traslación de un sistema de coordenadas

6. Conversión de coordenadas locales a globalesAplicación a robótica móvil

7. Conversión de coordenadas locales a globales (II)Aplicación a un brazo articuladol2=3l1=2

8. Representación en el espacioCoordenadas cartesianasCoordenadas cilíndricasCoordenadas esféricas

9. Representación en el espacio (II)Traslación de un sistema de coordenadas

10. Representación en el espacio (III)Rotaciones sobre sistema de coordenadas cartesianas globales

11. Representación en el espacio (IV)Existen 12 combinaciones de rotación independientes

12. Representación en el espacio (V)Ángulos XYZ ó Ángulos RPYÁngulos de balanceo (Roll), inclinación (Pitch) y orientación (Yall)Orden de rotación: X,Y,ZToolbox de Robótica: rpy2tr(, , )

13. Ángulos RPY Toolbox de Robótica: rpy2tr(, , )

14. Ángulos RPY como producto de rotaciones% Rotación RPY% (gamma, beta, alpha)TB=rpy2tr(pi/6,pi/4,pi/5)*TA;Las rotaciones se realizanalrededor de los ejes originales o globales

15. Representación en el espacio (VI)Combinación de traslación y rotaciónGiróscopo adjunto a un vehículo (, , )LateralFrontalSuperiorVariación angularw(rad/s)

16. Representación en el espacio (VII)Combinación de traslación y rotación

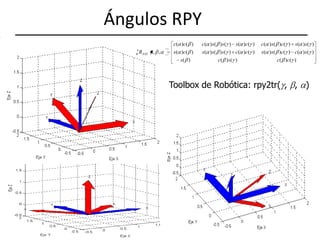
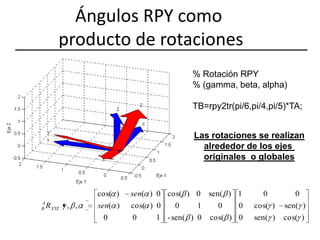
17. Representación en el espacio (VIII)Programa en Matlab>> porg=[3 4 5 0]'porg = 3 4 5 0>> pb=[-1 3 4 1]'pb = -1 3 4 1>> porg+rpy2tr(pi/6,pi/3,pi/8)*pbans = 6.2810 6.0064 8.3481 1.0000

18. Representación en el espacio (IX) ¿Posición del punto que representa el extremo del eslabón después de rotarprimero pi/2 en Y y después pi/6 en Z?El punto está en:Después de las dos rotaciones:

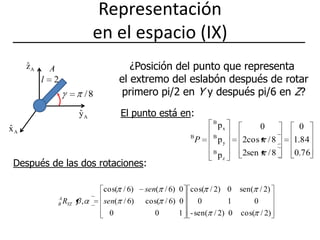
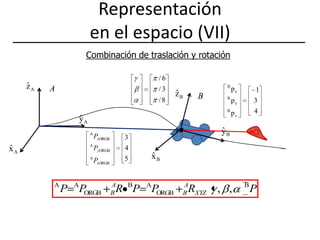
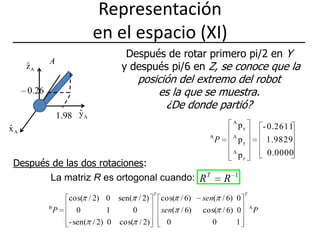
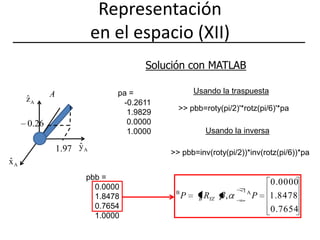
19. Representación en el espacio (X) Solución con MATLAB>> pb=[0 2*cos(pi/8) 2*sin(pi/8) 1]‘>> pa=rotz(pi/6)*roty(pi/2)*pbpa =-0.2611 1.9829 0.0000 1.0000

20. Representación en el espacio (XI) Después de rotar primero pi/2 en Yy después pi/6 en Z, se conoce que laposición del extremo del robot es la que se muestra. ¿De donde partió? Después de las dos rotaciones:La matriz R es ortogonal cuando:

21. Representación en el espacio (XII) Solución con MATLABUsando la traspuestapa=-0.2611 1.9829 0.00001.0000>> pbb=roty(pi/2)'*rotz(pi/6)'*paUsando la inversa>> pbb=inv(roty(pi/2))*inv(rotz(pi/6))*papbb= 0.0000 1.8478 0.7654 1.0000

22. Ángulos de RotaciónÁngulos (, , ) a partir de la matriz de rotación RPYSolución degeneradaEquivalencia entre la matriz de rotación y parámetros de Euler

23. Representación en el espacio (XI)Representación matricial de traslación y rotaciónMatriz de transformación homogéneaTraslaciónRotación

24. Definición de un cuadro de referencia origen% Se define una matriz % de transformación hogéneaTA=[ 1 0 0 0;0 1 0 0;0 0 1 0;0 0 0 1];% Visualización de la matrizframe(TA,'b',1);

25. Traslación de un sólido en el espacio% Se define matriz de transformación hogéneaTA=[1 0 0 0;0 1 0 0 ;0 0 1 0;0 0 0 1];% Traslación en xyzTB=transl(1,2,3)*TA;

26. Rotación de un sólido en el espacio% Se define matriz de % transformación hogéneaTA=[1 0 0 0;0 1 0 0 ;0 0 1 0;0 0 0 1];% Rotación en y 45 gradosTB=roty(pi/4)*TA;Matriz rotación

27. Rotación y traslación de un sólido en el espacio% Rotación en y 45 grados% y traslación xyzTB=transl(1,2,3)*roty(pi/4)*TA;frame(TA,'b',1.5);frame(TB,'r',1.5);axis([-1 3 -1 1 -1 5])

28. Representación en el espacio (XII)Inversión de la transformadaToolbox de Robótica: trinv(T)

29. Representación en el espacio (XIII)Matriz de transformación homogénea

30. Representación en el espacio (XIV)Ecuaciones de transformadas

31. Aplicación a brazos articuladosDeterminar la posición con respecto a la basel2=3l1=2

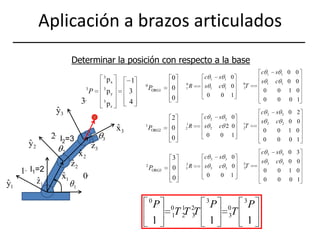
32. Aplicación a brazos articulados (II)Solución utilizando Matlab>> P3=[-1 3 4 1]'P3 = -1 3 4 1>> t=[pi/5 -pi/8 -pi/9]'t = 0.6283 -0.3927 -0.3491l2=3>> T01=[cos(t(1,1)) -sin(t(1,1)) 0 0;sin(t(1,1)) cos(t(1,1)) 0 0; 0 0 1 0; 0 0 0 1]>> T12=[cos(t(2,1)) -sin(t(2,1)) 0 2;sin(t(2,1)) cos(t(2,1)) 0 0; 0 0 1 0; 0 0 0 1] >> T23=[cos(t(3,1)) -sin(t(3,1)) 0 3;sin(t(3,1)) cos(t(3,1)) 0 0; 0 0 1 0; 0 0 0 1]>> P0=T01*T12*T23*P3P0 = 3.8812 4.9698 4.0000 1.0000l1=2Compararse con el robot Scara

33. Aplicación a robótica móvil

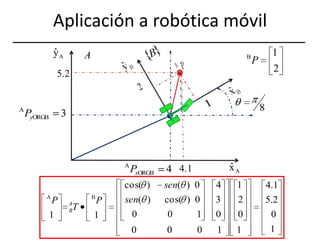
34. Aplicación a robótica móvil (II)Solución con MATLAB>> pb=[1 2 0 1]‘>> TBA=[cos(pi/8) -sin(pi/8) 0 4; sin(pi/8) cos(pi/8) 0 3; 0 0 1 0; 0 0 0 1]>> pa=TBA*pbpa= 4.1585 5.2304 0 1.0000

35. Ángulos de Euler Z-Y-XÁngulos RPY: Se rota relativo al sistema {A}Ángulos Euler: Se rota relativo al sistema {B} móvilSolución equivalente a los Ángulos RPYrpy2tr(, , )

36. Ángulos de Euler Z-Y-Zecho offdisp('Muestra de Ángulos de Euler Z-Y-Z')clear allTA=[1 0 0 0; 0 1 0 0 ; 0 0 1 0; 0 0 0 1];TB=eul2tr(45,0,0);frame(TA,'b',1);frame(TB,'r',1);

37. Ángulos de RotaciónEquivalencia entre la matriz de rotación y parámetros de EulerÁngulos ( , , ) a partir de la matriz de rotación Z-Y-ZSolución degenerada

38. Consideraciones computacionales Método A63 multiplicacionesy 42 sumasMétodo B27 multiplicacionesy 18 sumasFuente: Craig, J.: Robótica. Tercera edición. 2006