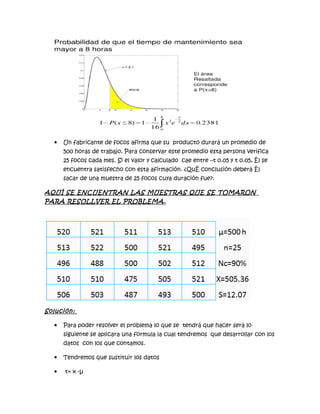
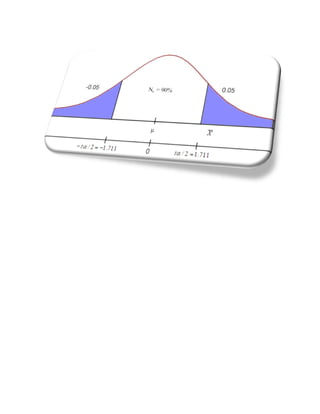
La distribución gamma se utiliza para modelar el tiempo hasta que ocurren ciertos eventos. Si el número de eventos sigue una distribución de Poisson, el tiempo hasta el enésimo evento sigue una distribución gamma. Esta distribución se usa en fiabilidad, mantenimiento y tiempos de espera. Los ejemplos incluyen el tiempo de vida útil y el tiempo hasta la llegada del segundo paciente a una consulta médica.

1. DISTRIBUCIÓN GAMMA
La distribución gamma se puede caracterizar del modo siguiente: si se está
interesado en la ocurrencia de un evento generado por un proceso de Poisson de
media lambda, la variable que mide el tiempo transcurrido hasta obtener n
ocurrencias del evento sigue una distribución gamma con parámetros a=
nnlambda(escala) y p=n (forma). Se denota
Gamma(a,p).
Por ejemplo, la distribución gamma aparece cuando se realiza el estudio de la
duración de elementos físicos (tiempo de vida).
Esta distribución presenta como propiedad interesante la “falta de memoria”. Por
esta razón, es muy utilizada en las teorías de la fiabilidad, mantenimiento y
fenómenos de espera (por ejemplo en una consulta médica “tiempo que transcurre
hasta la llegada del segundo paciente”).
Ejercicio 1
El número de pacientes que llegan a la consulta de un médico sigue una
distribución de
Poisson de media 3 pacientes por hora. Calcular la probabilidad de que transcurra
menos de una hora hasta la llegada del segundo paciente.
Debe tenerse en cuenta que la variable aleatoria “tiempo que transcurre hasta la
llegada del segundo paciente” sigue una distribución Gamma (6, 2).
Solución:
Cálculo de probabilidades. Distribuciones continuas
Gamma (a p)
a : Escala 60000
p : Forma 20000
Punto X 10000
Cola Izquierda Pr[X<=k] 0,9826
Cola Derecha Pr[X>=k] 0,0174
Media 0,3333
Varianza 0,0556
Moda 0,1667
La probabilidad de que transcurra menos de una hora hasta que llegue el segundo
paciente es 0,98.
Ejercicio 2

2. Suponiendo que el tiempo de supervivencia, en años, de pacientes que son
sometidos a una cierta intervención quirúrgica en un hospital sigue una
distribución Gamma con parámetros a=0,81 y p=7,81, calcúlese:
1. El tiempo medio de supervivencia.
2. Los años a partir de los cuales la probabilidad de supervivencia es menor que
0,1.
Cálculo de probabilidades. Distribuciones continuas
Gamma (a,p)
a : Escala 0,8100
p : Forma 7,8100
Cola Izquierda Pr [X<=k] 0,9000
Cola Derecha Pr [X>=k] 0,1000
Punto X 14,2429
Media 9,6420
Varianza 11,9037
Moda 8,4074
El tiempo medio de supervivencia es de, aproximadamente, 10 años.

5.  Un fabricante de focos afirma que su producto durará un promedio de
500 horas de trabajo. Para conservar este promedio esta persona verifica
25 focos cada mes. Si el valor y calculado cae entre –t 0.05 y t 0.05, él se
encuentra satisfecho con esta afirmación. ¿Qué conclusión deberá él
sacar de una muestra de 25 focos cuya duración fue?:
AQUÍ SE ENCUENTRAN LAS MUESTRAS QUE SE TOMARON
PARA RESOLLVER EL PROBLEMA.
Solución:
 Para poder resolver el problema lo que se tendrá que hacer será lo
siguiente se aplicara una formula la cual tendremos que desarrollar con los
datos con los que contamos.
 Tendremos que sustituir los datos
 t= x -μ

6.  SI n α = 1- Nc = 10%
 v = n-1 = 24
 t = 2.22
Procedimiento:se demostrara la forma en que se sustituiran los
datos.
 VALOR DE LOS DATOS. . APLICACION
DE LA FORMULA
 μ=500 h t=505.36-500 t = 2.22
 n=25 12.07 25
 Nc=90% v = 25 -1 = 24
 X=505.36 α = 1- 90% = 10%
 S=12.07
Enseguida se muestra la distribución del problema según el grafico
sig.