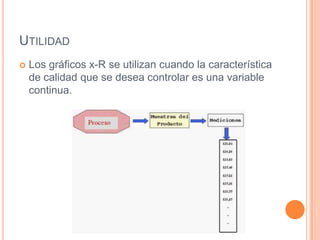
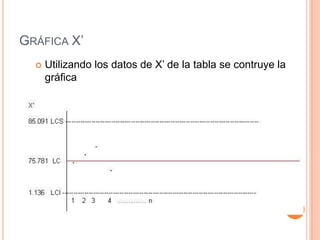
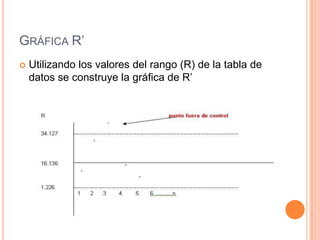
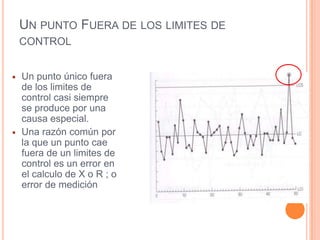
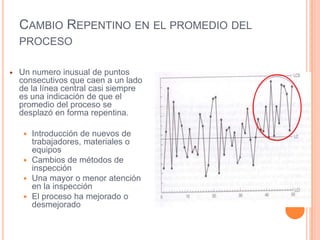
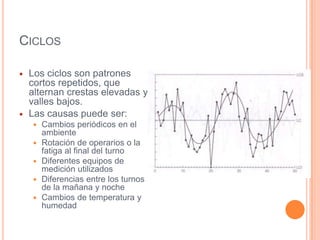
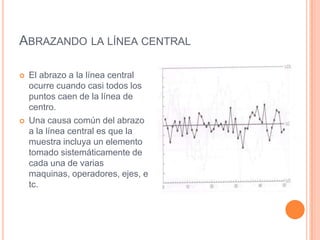
Este documento describe los gráficos de control, los cuales son diagramas utilizados para monitorear procesos de producción e identificar inestabilidad. Explica cómo construir gráficos X-R mediante la recolección y análisis de datos, y cómo interpretar los gráficos resultantes para detectar cambios en el proceso y asegurar la calidad.

1. GRAFICAS DE CONTROL

2. INTRODUCCIÓN
 Un gráfico de control es un
diagrama especialmente
preparado donde se van
anotando los valores sucesivos
de la característica de calidad
que se está controlando.
 Los datos se registran durante
el funcionamiento del proceso
de fabricación y a medida que
se obtienen.
 Las graficas de control se
utilizan en la industria como
técnica de diagnósticos para
 supervisar procesos de
producción e identificar
inestabilidad y circunstancias
anormales.

3. OBJETIVO GENERAL
 Todo grafico de control
esta diseñado para
presentar los siguientes
principios:
 Fácil de entendimiento de
los datos
 Claridad
 Consistencia
 Medir variaciones de
calidad

4. OBJETIVO ESPECÍFICO
 Proceso de prevención para evitar que el producto llegue
sin defectos al cliente.
 Detectar y corregir variaciones de calidad

5. ELECCIÓN DE LA VARIABLE
 La variable que se elija para los gráficos de control
X y R , tiene que ser una magnitud que pueda
medirse y expresarse con números, tal como la
dimensión, el grado de dureza, resistencia a la
tracción, peso, etc.

6. GRAFICOS X-R

7. UTILIDAD
 Los gráficos x-R se utilizan cuando la característica
de calidad que se desea controlar es una variable
continua.

8. 3. GRÁFICOS DE CONTROL POR
VARIABLES
Gráficos - R
Se utilizan cuando la característica de calidad que se
desea controlar es una variable continua.
Se requieren N muestras ( Subgrupos) de tamaño n.
 Ejemplo: fábrica que produce piezas cilíndricas de
madera. La característica de calidad que se desea
controlar es el diámetro. Hay dos maneras de
obtener los subgrupos. Una de ellas es retirar
varias piezas juntas a intervalos regulares, por
ejemplo cada hora:
x

9. PASO #1:RECOLECCIÓN DE DATOS
 Estos datos deberán
ser:
 Recientes de un
proceso al cual se
quiere controlar
 Estos pueden ser
tomados
 Diferentes horas del
día
 Diferentes días
 Todos tienen que ser
de un mismo producto.

10. PASO #2: PROMEDIO
 Sumatoria de los datos
de cada uno de los
subgrupos dividido entre
el numero de datos (n).
 Formula X
 ∑X1 + X2 + X3 + Xn
n
 La formula debe ser
utilizada para cada uno
de los subgrupos

11. PASO #3: RANGO
 Valor mayor del
subgrupo menor el
valor menor.
 Formula
 R = x valor mayor – x valor
menor
 Determine el rango
para cada uno de los
subgrupos

12. PASO #4: PROMEDIO GLOBAL
 Sumatoria de todos
los valores medios y
se divide entre el
número de subgrupos
(k).
 Formula X’
 ∑X1 + X2 + X3 +…+
Xn
k

13. PASO #5: VALOR MEDIO DEL RANGO
 Sumatoria del rango
(R) de cada uno de los
subgrupos divido entre
el numero de
subgrupos (k).
 Formula R’
 ∑R1 + R2 + R3 + …. +
Rn
k

14. PASO #6: LIMITES DE CONTROL
 Para calcular los limites de control se utilizan los
datos de la siguiente tabla

15. LIMITES DE CONTROL

16. GRÁFICA X’
 Utilizando los datos de X’ de la tabla se contruye la
gráfica

17. GRÁFICA R’
 Utilizando los valores del rango (R) de la tabla de
datos se construye la gráfica de R’

18. INTERPRETACIÓN DE LAS GRAFICAS
CONTROL

19. UN PUNTO FUERA DE LOS LIMITES DE
CONTROL
 Un punto único fuera
de los limites de
control casi siempre
se produce por una
causa especial.
 Una razón común por
la que un punto cae
fuera de un limites de
control es un error en
el calculo de X o R ; o
error de medición

20. CAMBIO REPENTINO EN EL PROMEDIO DEL
PROCESO
 Un numero inusual de puntos
consecutivos que caen a un lado
de la línea central casi siempre
es una indicación de que el
promedio del proceso se
desplazó en forma repentina.
 Introducción de nuevos de
trabajadores, materiales o
equipos
 Cambios de métodos de
inspección
 Una mayor o menor atención
en la inspección
 El proceso ha mejorado o
desmejorado

21. CAMBIO REPENTINO EN EL PROMEDIO DEL
PROCESO
 Se emplean tres reglas empíricas
para detectar a tiempo los cambios
de los procesos:
 Si 8 puntos consecutivos caen en
un lado de la línea central
 Se divide la región entre la línea
central y cada limite de control en
tres partes iguales. Luego, Si (1)
dos de tres puntos consecutivos
caen en el tercio exterior entre la
línea central y uno de los limites
de control o (2) cuatro de cinco
puntos consecutivos caen dentro
de la región exterior de dos
tercios, también se puede llegar
a la conclusión de que el proceso
esta fuera de control

22. CICLOS
 Los ciclos son patrones
cortos repetidos, que
alternan crestas elevadas y
valles bajos.
 Las causas puede ser:
 Cambios periódicos en el
ambiente
 Rotación de operarios o la
fatiga al final del turno
 Diferentes equipos de
medición utilizados
 Diferencias entre los turnos
de la mañana y noche
 Cambios de temperatura y
humedad

23. TENDENCIAS
 Una tendencia es el resultado de
alguna causa que afecta en forma
gradual las características de calidad
del producto y ocasiona que los
puntos de las graficas de control se
muevan gradualmente hacia arriba o
hacia abajo.
 Una tendencia definida se da:
 Deterioro o desgaste gradual de
un equipo de producción
 Desgaste de herramienta
 Acumulación desperdicios
 Calentamiento de maquinas
 Cambios graduales condiciones
ambientales
 Mejora en las habilidades del
operario

24. ABRAZANDO LA LÍNEA CENTRAL
 El abrazo a la línea central
ocurre cuando casi todos los
puntos caen de la línea de
centro.
 Una causa común del abrazo
a la línea central es que la
muestra incluya un elemento
tomado sistemáticamente de
cada una de varias
maquinas, operadores, ejes, e
tc.

25. ABRAZANDO LOS LIMITES DE CONTROL
 Este patrón aparece
cuando muchos puntos se
encuentran cerca de los
limites de control con muy
pocos entre dichos limites
 Las causas pueden ser:
 Un patrón de mezcla puede
resultar cuando en un
proceso se utilizan dos lotes
de material diferentes o
cuando las partes se
producen en distintas
maquinas , pero la vigila el
mismo grupo de inspección

26. INESTABILIDAD
 Se caracteriza por
flutaciones erráticas y
poco naturales en ambos
lados del cuadro durante
un tiempo. A menudo, los
puntos caen fuera de los
limites de control superior
e inferior sin un patrón
consistente. Una causa
frecuente de inestabilidad
es el ajuste excesivo de
una maquina