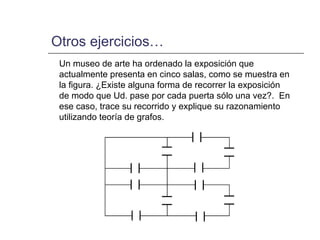
El documento trata sobre conceptos básicos de teoría de grafos como rutas, ciclos, grafos y vértices. Explica el problema de los puentes de Königsberg y cómo se puede modelar con un grafo. También presenta teoremas sobre la existencia de ciclos y rutas de Euler y Hamilton en función del grado de los vértices de un grafo. Finalmente, propone algunos ejercicios prácticos para determinar si es posible realizar ciertos recorridos pasando una sola vez por cada puerta o vértice.

1. Matemáticas Discretas Teoría de Grafos

2. Teoría de Grafos Rutas y Ciclos Euler Hamilton Algoritmo de DIJKSTRA (Ruta más corta)

3. Rutas y Ciclos de Euler Ruta de Euler Es un camino que pasa por todo arco (edge) solo una vez. Ciclo de Euler Es un ciclo que pasa por todo arco (edge) solo una vez.

4. Puentes de Königsberg El problema consiste en partir de cualquier lugar (A, B, C o D), caminar sobre cada puente exactamente una vez y regresar a la posición inicial. Puentes de Königsberg

5. Un modelo del grafo de los puentes de Königsberg: Puentes de Königsberg Los puentes son representados por arcos y los vértices representan a las orillas y a las islas.

6. Trazos ¿Es posible trazar las siguientes figuras sin levantar el lápiz?

7. Trazos ¿Y esta ?

8. Trazos ¿Y esta ?

9. Solución La solución al problema de existencia de Ciclos de Euler se puede establecer mediante el grado de un vértice . Definición El grado de un vértice es el número de arcos que tienen a ese vértice como extremo.

10. Teorema 1 (Sección 6.1 Kolman) (a) Si una gráfica G tiene un vértice de grado impar, entonces no puede existir un circuito de Euler en G. (b) Si G es una gráfica conexa y todos los vértices tienen grado par, entonces existe un circuito de Euler en G. Teorema 2 (Sección 6.1 Kolman) (a) Si una gráfica G tiene más de dos vértices de grado impar, entonces no puede existir una trayectoria de Euler en G. (b) Si G es conexa y tiene exactamente dos vértices de grado impar, entonces existe una trayectoria de Euler en G. Cualquier trayectoria de Euler debe comenzar en un vértice de grado impar y terminar en el otro. Rutas y Ciclos

11. Rutas y Ciclos de Euler

12. Rutas y Ciclos de Hamilton Ruta de Hamilton Es un camino que pasa por todo vértice solo una vez. Ciclo de Hamilton Es un ciclo que pasa por todo vértice solo una vez excepto el primer vértice que también es el último.

13. Rutas y Ciclos de Hamilton (a) Juego de Hamilton (b)Grafo de Juego de Hamilton (c) Visita de cada vértice una vez en el grafo

14. Rutas y Ciclos de Hamilton Grafo con Ciclo Hamilton Grafo sin Ciclo Hamilton

15. Otros ejercicios… Considere el plano de una estructura con tres cuartos, como muestra la figura: ¿Es posible comenzar en un cuarto o en el exterior y dar la vuelta de modo que se pase por cada puerta sólo una vez?

16. Otros ejercicios… Un museo de arte ha ordenado la exposición que actualmente presenta en cinco salas, como se muestra en la figura. ¿Existe alguna forma de recorrer la exposición de modo que Ud. pase por cada puerta sólo una vez?. En ese caso, trace su recorrido y explique su razonamiento utilizando teoría de grafos.