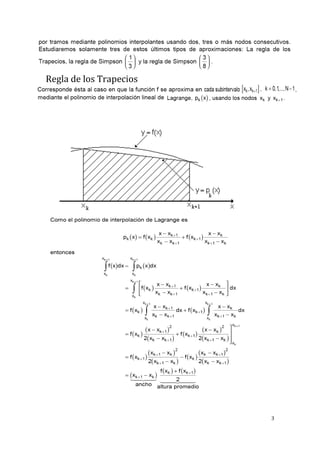
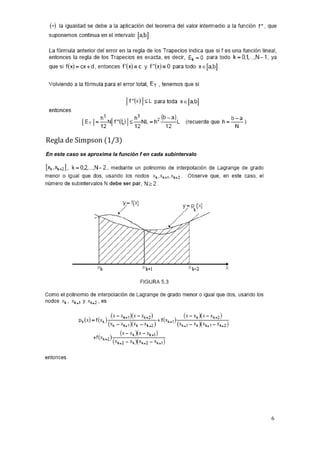
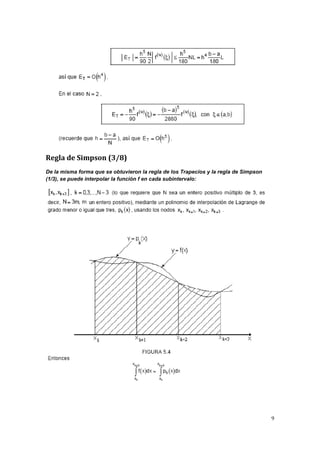
Este documento describe diferentes reglas para la integración numérica, incluyendo la regla de los trapecios, la regla de Simpson (1/3) y la regla de Simpson (3/8). También presenta ejemplos de cómo usar estas reglas para estimar integrales definidas y calcular la longitud de un arco de curva, así como los valores de n y h necesarios para aproximar una integral con un error menor a un valor dado usando la regla de Simpson (1/3). Finalmente, introduce el método de integración de Romberg.

1. 1
INTEGRACION NUMERICA

2. 2
Formulas cerradas de Newton-Cotes

3. 3
Regla de los Trapecios

4. 4

5. 5

6. 6
Regla de Simpson (1/3)
En este caso se aproxima la función f en cada subintervalo

7. 7

8. 8

9. 9
Regla de Simpson (3/8)
De la misma forma que se obtuvieron la regla de los Trapecios y la regla de Simpson
(1/3), se puede interpolar la función f en cada subintervalo:

10. 10

11. 11
Ejemplo:
1. Use las reglas de los Trapecios, Simpson (1/3) y
Simpson(3/8) simples y compuestas con N=6 para estimar:
Dar una cota para el error en la estimación, en cada caso
(desprecie los errores de redondeo)

12. 12

13. 13

14. 14

15. 15

16. 16

17. 17

18. 18
2) Use la regla de Simpson (1/3) con N=6 para estimar la longitud L del arco de la
curva comprendida entre los puntos
Se trata de resolver:

19. 19
3) Determine los valores de n y h necesarios para aproximar:
De manera que el error en la aplicación de la regla de Simpson (1/3) no sea
mayor que y determine la aproximación (desprecie los errores de
redondeo)

20. 20

21. 21
Integración de Romberg

22. 22

23. 23

24. 24

25. 25

26. 26
EJERCICIOS

27. 27
5.
6.

28. 28
7.