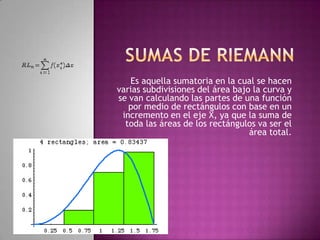
El documento explica el concepto de suma de Riemann para calcular áreas bajo la curva utilizando rectángulos. Se ejemplifica su aplicación en la función f(x)=2x+3 en el intervalo [1,4], y se concluye que el área aproximada es 24u². Además, se menciona que este resultado se puede comprobar mediante integrales.

1. Es aquella sumatoria en la cual se hacen
varias subdivisiones del área bajo la curva y
se van calculando las partes de una función
por medio de rectángulos con base en un
incremento en el eje X, ya que la suma de
toda las áreas de los rectángulos va ser el
área total.

2. Límites:
Evaluando la suma de Riemann en cuatro
subintervalos tomando los puntos de la
derecha de la siguiente función:
ƒ(0.5)=2-(0.5)²
=2-0.25
=1.75
La suma de Riemann representa la suma
de las áreas sobre el eje , menos la suma
de las áreas debajo del eje ; esa es el área
neta de los rectángulo respecto al eje .

3. Función:
f(X)=2X+3
LIMITES:
[1,4]
Valores a
Sustituir.
Formula:
Sustitución en
la función.
Las formulas para calcular la
siguiente área son las
siguientes:

4. 0
Ahora que terminamos todo el procedimiento
y que sabemos que el área aproximada es
igual 24u² podremos comprobar el resultado
por medio de integrales.
Área

5. Con la comprobación pudimos
comprobar que nuestra primera
afirmación es similar.
Área