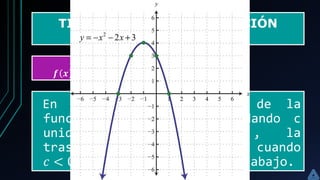
Este documento presenta información sobre las funciones cuadráticas. Explica que una función cuadrática es una función polinómica de grado 2 de la forma f(x)=ax2+bx+c. Describe las características de la gráfica de una función cuadrática, la cual es una parábola. También detalla los cuatro tipos de gráficas de funciones cuadráticas y resuelve ejemplos para ilustrar cómo graficar cada tipo. El objetivo es que los estudiantes comprendan las propiedades de las funciones cuadráticas y cómo

1. FUNCIÓN
CUADRÁTICA
GIMNASIO CAMPESTRE
GRADO:9´S
2018

2. OBJETIVO GENERAL
• Comprender las
características
de la función
cuadrática y su
representación
grafica.

3. OBJETIVOS ESPECÍFICOS
❑Identificar las características de
una función cuadrática.
❑Comprender los tipos de graficas
de funciones cuadráticas.
❑Graficar una función cuadrática.

4. CONTENIDO ASOCIADOS
❑Función Cuadrática.
❑Gráfica de una función cuadrática.
❑Tipos de gráfica de función
cuadrática.
Fecha: 18 Septiembre/2017
Duración: 110 Min

5. COMENCEMOS….
Un terreno es
cuadrangular y
sabemos que
mide de área
169 metros
cuadrados,
¿cuánto miden
sus lados?

6. RESPONDAMOS…
¿Las funciones
cuadráticas para
que se usan ó
aplican en el
campo de la
ingeniería civil?
¿Las funciones
cuadráticas para
que se usan ó
aplican en el
campo de la
biología?

7. ANALICEMOS UN FENOMENO DE LA
NATURALEZA
Juan esta visitando un lugar turístico en su
ciudad, donde una de las atracciones son algunas
fuentes iluminadas por varios reflectores de
diferentes colores.
Juan se interesa en una de las fuentes, la cual
lanza chorros de agua verticales, con velocidad de
20m/s. Uno de los operarios dice que la altura del
agua en metros para un tiempo t en segundos se
puede hallar con la siguiente expresión:
𝒇 𝒕 = −𝟓𝒕 𝟐 + 𝟐𝟎𝒕

8. RESOLVAMOS…
1. Juan quiere saber a que altura se encuentra el
chorro de agua, un segundo después de ser
lanzado.
2. Juan observa que el chorro de agua llega a
cierto punto y vuelve a caer. Cuánto tiempo
tarda en llegar a ese punto?
3. ¿A qué altura se encuentra el agua en su punto
máximo?
4. ¿Cuánto tiempo le toma a un chorro de agua subir
y volver al suelo?

9. GRAFICADORES

10. FUNCIÓN CUADRÁTICA
Una función cuadrática es una función que puede ser descrita
por una ecuación de la forma 𝒇 𝒙 = 𝒂𝒙 𝟐
+ 𝒃𝒙 + 𝒄, donde a ≠ 0.
Ningún término en la función polinomial tiene un grado mayor
que 2. Las funciones cuadráticas son útiles cuando
trabajamos con áreas, y frecuentemente aparecen en problemas
de movimiento que implican gravedad o aceleración. Una
función cuadrática es un polinomio de grado 2, es decir, el
exponente más alto en la variable es 2.

11. GRÁFICA DE UNA FUNCIÓN
CUADRÁTICA
Al graficar una función cuadrática se obtiene una
curva llamada parábola.
Para graficar una función cuadrática de la forma
𝒇 𝒙 = 𝒂𝒙 𝟐 + 𝒃𝒙 + 𝒄 , se debe tener en cuenta:
- Si 𝑎 > 0 , la parábola abre hacia arriba y la
función tiene un mínimo que es el vértice (h,k)
- Si 𝑎 < 0 , la parábola abre hacia abajo y la
función tiene un máximo que es el vértice (h,k)
- C es el corte de la parábola con el eje Y.

12. (h,k)
(h,k)
Máximo
Mínimo

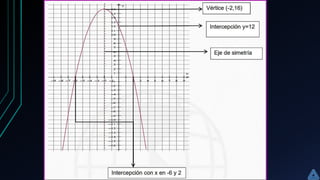
13. Las coordenadas del vértice V se representan V(h,k) y se
determinan mediante las siguientes expresiones:
𝒉 = −
𝒃
𝟐𝒂
𝒌 = 𝒇 −
𝒃
𝟐𝒂
El dominio de una función cuadrática es el conjunto de
los números reales R, y el rango es el intervalo,[k,∞) si
la parábola abre hacia arriba ó es (−∞, 𝑘] si la parábola
abre hacia abajo.
La recta paralela al eje Y, que pasa por le vértice de
parábola, se denomina eje de simetría.
𝒙 = −
𝒃
𝟐𝒂

15. TIPOS DE GRÁFICA DE
FUNCIÓN CUADRÁTICA
Según los valores de a, b
y c en la expresión
𝒇 𝒙 = 𝒂𝒙 𝟐
+ 𝒃𝒙 + 𝒄 , hay
cuatro casos que se
pueden tener en cuenta
para graficar una función
cuadrática.
1. 𝑓 𝑥 = 𝑥2
2. 𝑓 𝑥 = 𝑎𝑥2 + 𝑐
3. 𝑓 𝑥 = 𝑎𝑥2 + 𝑏𝑥
4. 𝑓 𝑥 = 𝑎𝑥2 + 𝑏𝑥 + 𝑐

16. TIPOS DE GRÁFICA DE FUNCIÓN
CUADRÁTICA
CASO 1:
𝒇 𝒙 = 𝒙 𝟐, 𝒃 = 𝟎 𝒚 𝒄 = 𝟎
Vértice (0,0) y eje de simetría es y.
▪ Si 𝑎 > 0, 𝑙𝑎 𝑝𝑎𝑟𝑎𝑏𝑜𝑙𝑎 𝑎𝑏𝑟𝑒 ℎ𝑎𝑐𝑖𝑎 𝑎𝑟𝑟𝑖𝑏𝑎.
▪ Si 𝑎 < 0, 𝑙𝑎 𝑝𝑎𝑟𝑎𝑏𝑜𝑙𝑎 𝑎𝑏𝑟𝑒 ℎ𝑎𝑐𝑖𝑎 𝑎𝑏𝑎𝑗𝑜.

17. TIPOS DE GRÁFICA DE FUNCIÓN
CUADRÁTICA
CASO 2:
𝒇 𝒙 = 𝒂𝒙 𝟐
+ 𝒄, 𝒃 = 𝟎
Vértice (0,c) y eje de simetría es y.
▪ Si 𝑐 > 0, 𝑙𝑎 𝑡𝑟𝑎𝑠𝑙𝑎𝑐𝑖ó𝑛 𝑒𝑠 ℎ𝑎𝑐𝑖𝑎 𝑎𝑟𝑟𝑖𝑏𝑎.
▪ Si 𝑐 < 0, 𝑙𝑎 𝑡𝑟𝑎𝑠𝑙𝑎𝑐𝑖ó𝑛 𝑒𝑠 ℎ𝑎𝑐𝑖𝑎 𝑎𝑏𝑎𝑗𝑜.
La grafica de esta función se obtiene
trasladando la grafica de la función
𝒇 𝒙 = 𝒂𝒙 𝟐
, 𝒄 𝒖𝒏𝒊𝒅𝒂𝒅𝒆𝒔.

18. TIPOS DE GRÁFICA DE FUNCIÓN
CUADRÁTICA
CASO 3:
𝒇 𝒙 = 𝒂𝒙 𝟐
+ 𝒃𝒙, 𝒄 = 𝟎
Vértice (h,k) y eje de simetría
es x.

19. TIPOS DE GRÁFICA DE FUNCIÓN
CUADRÁTICA
CASO 4:
𝒇 𝒙 = 𝒂𝒙 𝟐
+ 𝒃𝒙 + 𝒄
En este caso la grafica de la
función se obtiene trasladando c
unidades. Cuando 𝑐 > 0 , la
traslación es hacia arriba y cuando
𝑐 < 0 la traslación es hacia abajo.

20. PRACTIQUEMOS LO VISTO….
Graficar las funciones
cuadráticas 𝑓 𝑥 = 5𝑥2 +
3𝑥 − 9, g 𝑥 = 5𝑥2 + 3𝑥 − 9,
h 𝑥 =
1
3
𝑥2 , en el mismo
plano cartesiano. Luego,
compáralas con respecto
a la función 𝑓 𝑥 = 𝑥2

21. PRACTIQUEMOS LO VISTO….
Graficar las funciones
cuadráticas:
a. 𝑓 𝑥 = 4𝑥2
− 2
b. 𝑓 𝑥 = −2𝑥2
− 8𝑥
c. 𝑓 𝑥 = −2𝑥2 − 4𝑥 − 4

22. APLIQUEMOS LO APRENDIDO EN
CLASE…
Resuelve las
actividades de
planteadas en el
archivo llamado
taller de función
cuadrática
alojado en la
plataforma
virtual del
curso.

23. Muchas Gracias
FIN DE LA CLASE