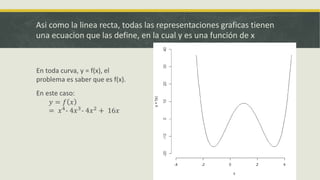
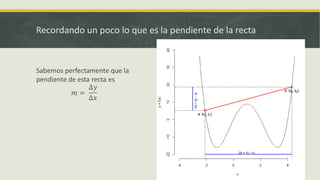
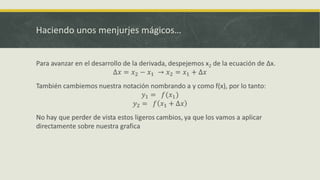
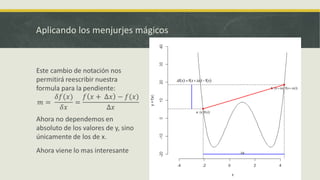
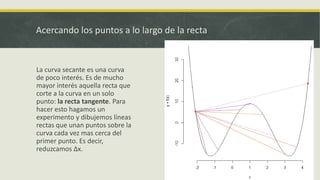
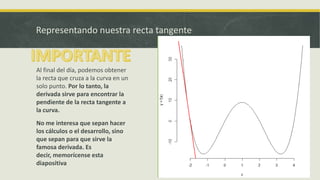
Este documento explica la derivada y sus aplicaciones. Introduce la derivada como una herramienta para encontrar la pendiente de la recta tangente a una curva en un punto, lo que sirve para calcular tasas de cambio instantáneas y optimizar funciones. También discute cómo la derivada puede usarse para ahorrar tiempo en cálculos y encontrar valores máximos, mínimos y puntos de inflexión.

1. Abril 5, 2013 Jhosse Paul Márquez Ruíz
Métodos estadísticos
La derivada
Desarrollo y explicación de la gran temida en el cálculo
Presentación fool’s proof

2. Requisitos previos
Haber leido las diapositivas de linea recta

3. Asi como la linea recta, todas las representaciones graficas tienen
una ecuacion que las define, en la cual y es una función de x

4. La línea secante
Ahora que conocemos la línea
recta, podemos definir rectas
especificas que unan
exactamente dos puntos de
nuestra curva.
Estas líneas se conocen como
líneas secantes.
Y como todas las rectas tiene
ciertas propiedades que ya
hemos estudiado. En particular
podemos calcular su pendiente
de manera sencilla.

5. Recordando un poco lo que es la pendiente de la recta

6. Haciendo unos menjurjes mágicos…

7. Aplicando los menjurjes mágicos

8. Acercando los puntos a lo largo de la recta
La curva secante es una curva
de poco interés. Es de mucho
mayor interés aquella recta que
corte a la curva en un solo
punto: la recta tangente. Para
hacer esto hagamos un
experimento y dibujemos líneas
rectas que unan puntos sobre la
curva cada vez mas cerca del
primer punto. Es decir,
reduzcamos ∆x.

9. Haciendo uso de la definición de limite

10. Representando nuestra recta tangente
Al final del día, podemos obtener
la recta que cruza a la curva en un
solo punto. Por lo tanto, la
derivada sirve para encontrar la
pendiente de la recta tangente a
la curva.
No me interesa que sepan hacer
los cálculos o el desarrollo, sino
que sepan para que sirve la
famosa derivada. Es
decir, memorícense esta
diapositiva

11. Aplicaciones de la derivada
La derivada nos permite ahorrarnos mucho tiempo realizando cálculos lentos. Por
ejemplo, es mas sencillo calcular una raíz cuadrada con derivadas que
resolviéndola a mano.
La derivada, al ser una pendiente, es un indicador directo de la razón de cambio
instantánea de la función, es decir, nos dice cuando cambia hacia la siguiente
unidad la curva. Esta relación es exactamente la que conserva la velocidad y la
aceleración, o el incremento instantáneo de los precios en el Mercado.
La aplicación mas importante de la derivada es el calculo de valores
máximos, mínimos y puntos de inflexión, lo cual la convierte en una ponderosa
herramienta de optimización. En la estadística, la optimización es un recurso
importante para la estimación de parámetros poblacionales.