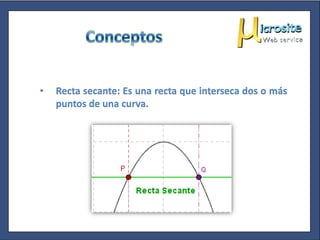
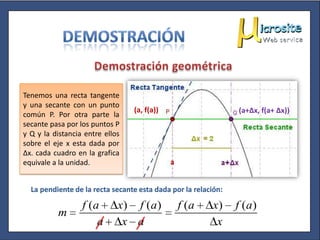
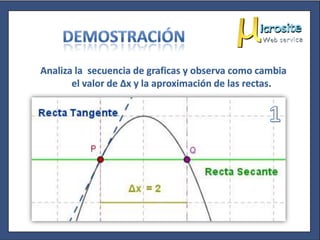
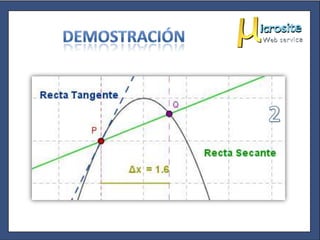
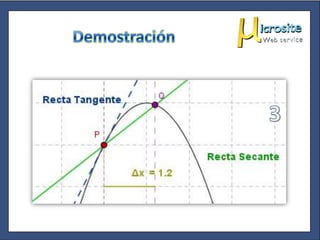
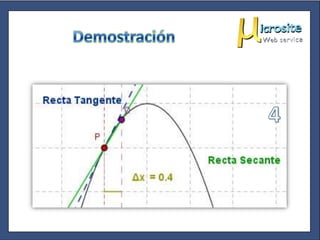
Este documento explica la diferencia entre una recta tangente y una recta secante a una curva, y cómo el cálculo del límite de la pendiente de una recta secante a medida que se aproxima a un punto da la pendiente de la tangente en ese punto, lo que define geométricamente la derivada.

1. Desarrollado por
Esp. Oscar Ardila Chaparro

2. Confuso ?

3. En la grafica se muestra
como ejemplo la recta
tangente a una
circunferencia (nótese que
solo existe un punto de
intersección entre los
objetos matemáticos).

4. Notación:
y
m
x
y2 y1
m
x2 x1

5. • Recta secante: Es una recta que interseca dos o más
puntos de una curva.

6. Si tenemos claros los conceptos en
los cuales se fundamenta la
definición su comprensión será muy
sencilla

7. Tenemos una recta tangente
y una secante con un punto
(a, f(a)) (a+∆x, f(a+ ∆x))
común P. Por otra parte la
secante pasa por los puntos P
y Q y la distancia entre ellos
sobre el eje x esta dada por
∆x. cada cuadro en la grafica
equivale a la unidad.
f (a x) f (a) f (a x) f (a)
m
a x a x

13. Se lee derivada de d ( f ( x)) f (a x) f (a)
f(x) evaluada en lim
términos de x. dx x 0 x
A medida que ∆x tiende a cero la recta secante se aproxima a la recta
tangente. Si esto es correcto podemos afirmar que el calculo del limite y la
relación planteada es equivalente al calculo de la pendiente de la recta
tangente a la curva f(x) en el punto P establecido (definición geométrica de la
derivada).

14. Esperamos que esta información oriente un poco tu proceso de
familiarización con el entorno y el seguimiento de cursos en
plataforma.
Desarrollado por
Esp. Oscar Ardila Chaparro