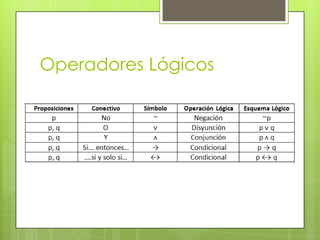
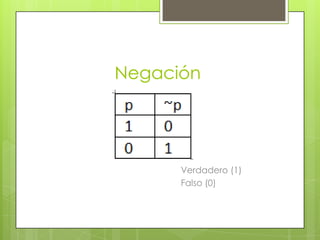
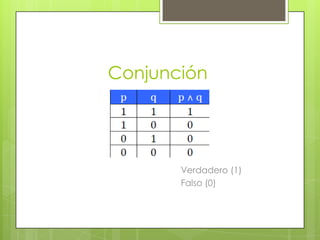
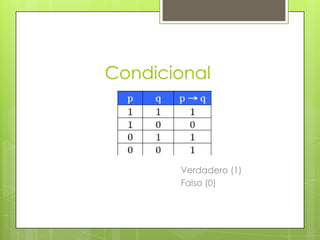
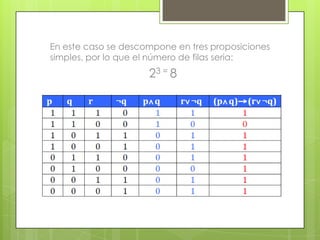
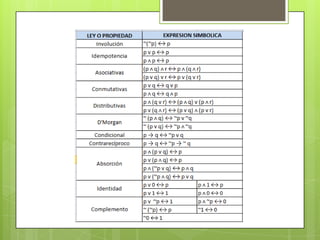
Este documento describe la lógica proposicional. Define una proposición como una expresión con sentido en un lenguaje que puede calificarse como verdadera o falsa. Explica que las proposiciones pueden ser simples o compuestas. Introduce los operadores lógicos como la negación, conjunción, disyunción y condicional y cómo se representan en una tabla de verdad. Finalmente, define tautologías, contradicciones y contingencias.

1. Lógica
proposicional
Por: Jessica Correa

2. Proposición
Expresión con sentido en un
lenguaje, a la que se puede
calificar sin ambigüedad si es
verdadera o falsa

3. EJEMPLOS
(1) Es una proposición ya que
sabemos con certeza que es
verdadero.
(2) También es una proposición
ya que es falso.
(3) Es una proposición debido a
que se sabe que es
verdadero.
(4) No es una proposición
porque no se la puede
calificar como verdadero o
falso, puesto que no se
conoce el valor de x.
(5) No es una proposición ya
que es una orden por lo
tanto no se la puede
calificar.

4. Clasificación:
Simples
compuestas

5. Proposiciones Simples
Cuando no se puede descomponer en dos
o mas proposiciones
EJEMPLO:
6 es múltiplo de 3

6. Proposiciones
compuestas
Cuando se puede descomponer en dos o mas
proposiciones simples
EJEMPLO:
p= el triangulo ABC es rectángulo o es oblicuángulo
Esta proposición se descompone en:
q= El triangulo ABC es rectángulo.
r= El triangulo ABC es oblicuángulo.

7. Operadores Lógicos

8. Algebra
Proposicional

9. Negación
Verdadero (1)
Falso (0)

10. Conjunción
Verdadero (1)
Falso (0)

11. Disyunción
Verdadero (1)
Falso (0)

12. Condicional
Verdadero (1)
Falso (0)

13. Bicondicional
Verdadero (1)
Falso (0)

14. ¿cómo construir una
tabla de verdad?
Para saber el número de filas de la tabla es 2n en
donde n es el numero de proposiciones simples que
intervienen en el esquema.

15. En este caso se descompone en tres proposiciones
simples, por lo que el número de filas seria:
23 = 8

16. CONTINGENCIAS,
TAUTOLOGÍAS Y
CONTRADICCIONES

17. TAUTOLOGÍAS
Todo esquema proposicional
que siempre es verdadero,
para cualquier valor de verdad
que se le asigne a las variables.

18. CONTRADICCIÓN
Todo esquema proposicional
que siempre es falso, para
cualquier valor de verdad que
se le asigne a las variables.

19. CONTIGENCIA
Todo esquema proposicional
que en la columna de
resultado es verdadero y falso.

20. LEYES O PROPIEDADES

22. Ejemplo
Utilizando las leyes del algebra proposicional
demostrar que:

23. INFERENCIA
LÓGICA

25. EJEMPLO
Hallar la conclusión: