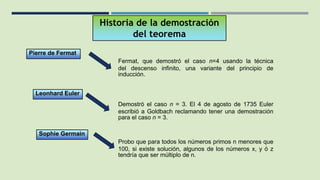
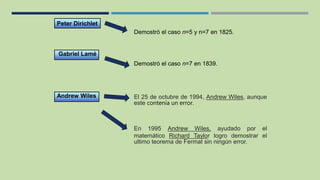
El documento describe la historia de la demostración del Último Teorema de Fermat, que establece que no existen números enteros positivos x, y, z que satisfagan la ecuación x^n + y^n = z^n para cualquier número entero n mayor que 2. Explica que Fermat afirmó el teorema pero no lo probó, y que fue demostrado gradualmente para casos particulares por matemáticos como Euler, Germain y Dirichlet, hasta que finalmente Wiles lo probó completamente en 1995.

1. Último Teorema de
Fermat

2. Si n es un número entero mayor
que 2, entonces no existen
números enteros positivos x, y, z,
tales que se cumpla la igualdad:
Definición:

3. Historia de la demostración
del teorema
Pierre de Fermat
Fermat, que demostró el caso n=4 usando la técnica
del descenso infinito, una variante del principio de
inducción.
Leonhard Euler
Demostró el caso n = 3. El 4 de agosto de 1735 Euler
escribió a Goldbach reclamando tener una demostración
para el caso n = 3.
Sophie Germain
Probo que para todos los números primos n menores que
100, si existe solución, algunos de los números x, y ó z
tendría que ser múltiplo de n.

4. Gabriel Lamé
Demostró el caso n=7 en 1839.
Peter Dirichlet
Demostró el caso n=5 y n=7 en 1825.
Andrew Wiles El 25 de octubre de 1994, Andrew Wiles, aunque
este contenía un error.
En 1995 Andrew Wiles, ayudado por el
matemático Richard Taylor logro demostrar el
ultimo teorema de Fermat sin ningún error.

5. Ejemplo:
3 = 4 – 1 =
7 = 16 – 9 =
22 - 12
32 - 42
Todo número primo impar puede ser expresado como la diferencia de
dos cuadrados de una sola forma.
Exprese cada uno de los siguientes primos impares como la diferencia
de dos cuadrados.
(b) 7
(a) 3

6. Muchas Gracias