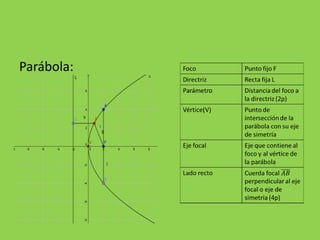
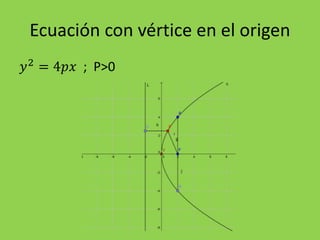
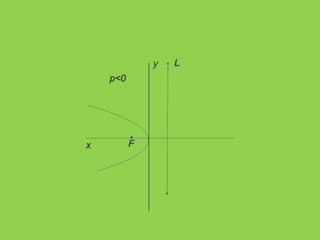
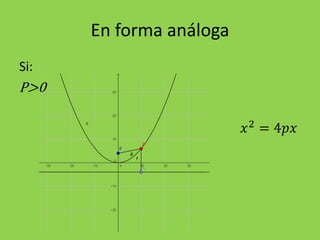
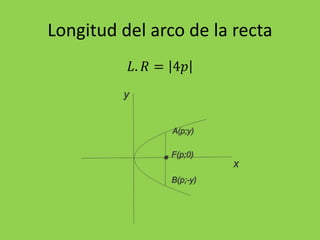
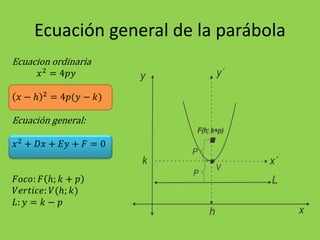
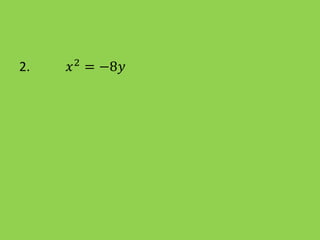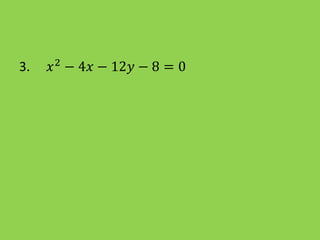La parábola es la curva formada por los puntos equidistantes de un punto fijo llamado foco y una recta llamada directriz. Se caracteriza por tener una ecuación de la forma y2=4px o x2=4py, donde p es un número positivo. El documento explica las ecuaciones generales de la parábola, cómo encontrar las coordenadas del vértice y foco, y resuelve varios ejercicios prácticos que implican hallar estas características y graficar parábolas.

1. La parábola
- Conjunto de puntos equidistantes de un punto
fijo (foco) y de una recta(directriz).
- Si: 𝑃 𝑥; 𝑦 → 𝑑 𝑝; 𝑓𝑜𝑐𝑜 = 𝑑 𝑝; 𝑑𝑖𝑟𝑒𝑐𝑡𝑟𝑖𝑧 = 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡𝑒

2. Parábola:

3. Ecuación con vértice en el origen
𝑦2
= 4𝑝𝑥 ; P>0

5. En forma análoga
Si:
P>0
𝑥2
= 4𝑝𝑥

7. Longitud del arco de la recta
𝐿. 𝑅 = 4𝑝

8. ejercicios
1.- para cada una de las parábolas ,determina
las coordenadas del foco, una ecuación de la
directriz, la longitud del lado recto y dibujar la
curva.
a) 𝑦2
= 8
b) 𝑦2
+ 6𝑥 = 0
c) 𝑥2
− 𝑦 = 0
d) 2𝑥2
+ 5𝑦 = 0

9. Ecuación general de la parábola
ecuación ordinaria:
𝑦2
= 4𝑝𝑥
𝑦 − 𝑘 2
= 4𝑝(𝑥 − ℎ)
ecuación general:
𝑦2
+ 𝐷𝑥 + 𝐸𝑦 + 𝐹 = 0
𝐹𝑜𝑐𝑜: 𝐹 ℎ + 𝑝; 𝑘
𝑉𝑒𝑟𝑡𝑖𝑐𝑒: 𝑉 ℎ; 𝑘
𝐿: 𝑥 = ℎ − 𝑝

10. Ecuación general de la parábola
Ecuacion ordinaria
𝑥2 = 4𝑝𝑦
𝑥 − ℎ 2
= 4𝑝(𝑦 − 𝑘)
Ecuación general:
𝑥2 + 𝐷𝑥 + 𝐸𝑦 + 𝐹 = 0
𝐹𝑜𝑐𝑜: 𝐹 ℎ; 𝑘 + 𝑝
𝑉𝑒𝑟𝑡𝑖𝑐𝑒: 𝑉(ℎ; 𝑘)
𝐿: 𝑦 = 𝑘 − 𝑝

11. Ejercicios
1.- dada la ecuación general de la
parabola,encontrar:
- Las coordenadas del vértice
- Las coordenadas del foco
- La ecuación de la directriz
- Trazar la grafica
i) 𝑦2
− 8𝑥 + 6𝑦 + 25 = 0
ii) 𝑥2
− 4𝑥 − 2𝑦 + 10 = 0

12. 2.- determina la ecuación ordinaria ,general y la
grafica de la parábola ,de acuerdo a los
siguientes datos:
i) 𝑑𝑖𝑟𝑒𝑐𝑡𝑟𝑖𝑧: 𝑦 = 1 ; 𝑓𝑜𝑐𝑜(−3; 7)
ii) 𝐹𝑜𝑐𝑜(1; 3) ; 𝑣é𝑟𝑡𝑖𝑐𝑒(−2; 3)

13. Pagina 370
obtenga las coordenadas del vértice, foco,
ecuación de la recta directriz, longitud del lado
recto y la grafica de:
1. 𝑦2
= 4𝑥

14. 2. 𝑥2
= −8𝑦

15. 3. 𝑥2
− 4𝑥 − 12𝑦 − 8 = 0

16. 4. 𝑦2
+ 6𝑦 + 4𝑥 − 7 = 0

17. Halla la ecuación de la parábola y su grafico de:
5. 𝑣𝑒𝑟𝑡𝑖𝑐𝑒: 𝑉 1; 2 𝑓𝑜𝑐𝑜: 𝐹 1; 6

18. 6. 𝑣𝑒𝑟𝑡𝑖𝑐𝑒: 𝑉 −2; 0
𝑟𝑒𝑐𝑡𝑎 𝑑𝑖𝑟𝑒𝑐𝑡𝑟𝑖𝑧: 𝐿𝐷: 𝑥 = −4

19. 7. Foco :F(-5;2)
Recta directriz :LD:y=6

20. 8.- vértice(6;3)
Eje focal paralelo a 𝑦 pasa por el punto :P(4;7)

21. En cada caso resuelve las situaciones
indicadas
9. Halla la ecuación general de la parábola cuyo
vértice coincide con el centro de la
circunferencia 𝑥2
+ 𝑦2
− 8𝑥 − 2𝑦 + 16 = 0
Y pasa por el origen de coordenadas siendo su
eje focal paralelo al eje de ordenadas.