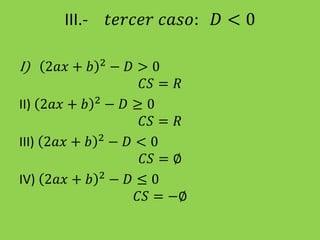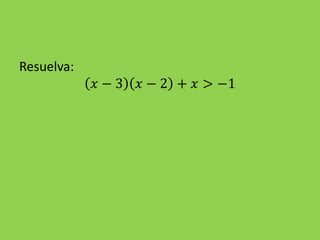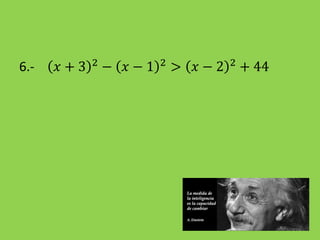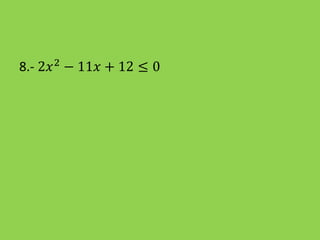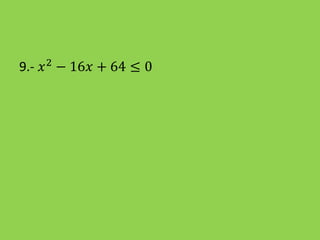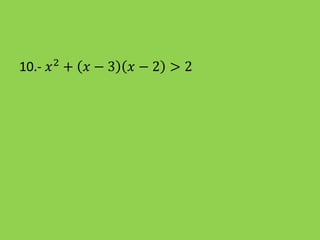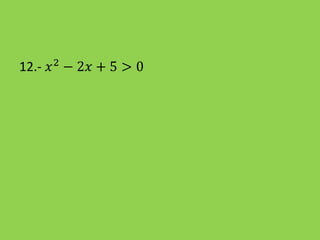Este documento presenta información sobre la resolución de inecuaciones cuadráticas. Explica los conceptos clave como el discriminante, los puntos críticos y los tres casos posibles para resolver una inecuación cuadrática dependiendo del signo del discriminante. También incluye ejemplos resueltos de inecuaciones cuadráticas.

1. • 2.- resuelve:
•
6(𝑥−4)
5
−
2(𝑥−4)
3
>
5𝑥−7
15

2. • 3.- resuelve
• 3 𝑥 − 4 + 5 𝑥 − 2 < 2 𝑥 − 6 − 4 5 − 𝑥

3. • 4.- resuelve:
• 3𝑥 − 2𝑥 − 1 ≤ 7𝑥 − 3 − 5𝑥 − 𝑥 + 24

4. • 5.- resuelve:
• 1 ≤
𝑥+2
𝑥+4
≤ 2

5. • 6.- resuelve:
• −1 <
𝑥+5
5
− 1 < 2

6. • 7.- indica la cantidad de valores enteros de x
que satisfacen la inecuación.
• −4𝑥 − 5 ≤ 2𝑥 + 7 < 𝑥 + 16

7. • 8.- el mínimo valor de x que satisface la
inecuación
• 𝑥 +
2𝑥
3
+
𝑥
2
≥
𝑎+5
12
, es 2 . Halla x

8. • 9.- resuelve:
•
5
3
<
2𝑥−3
3
< 3

9. • 10.- resuelve:
• 4 <
𝑥+2
𝑥+5
<
9
2

10. • 11.- resuelve el sistema
•
4𝑥+7
5
>
4𝑥−5
6
2
3
𝑥 − 1 ≥ 𝑥 + 4

11. • 12.- resuelve el sistema
•
𝑥
2
+
𝑥−1
3
< 𝑥 + 2
4 𝑥 − 5 +
1
2
𝑥 < 25

12. Inecuaciones cuadráticas
• Forma general:
• 𝑃 𝑥 = 𝑎𝑥2
+ 𝑏𝑥 + 𝑐 ≶ 0
• Donde:
• 𝑎, 𝑏, 𝑐 ∈ 𝑅 ∧ 𝑎 ≠ 0
• El símbolo ≶ representa a cualquiera de estos
cuatro: >, <, ≤, ≥

13. Discriminante(D)
• 𝐷 = 𝑏2
− 4𝑎𝑐
• Resolución general de la inecuación de
segundo grado.
• (2𝑎𝑥 + 𝑏)2
−𝐷 ≶ 0
• Nota:
• Depende del signo de la D o si D>0.

14. I.- Primer caso:D>0
• (2𝑎𝑥 + 𝑏)2
−𝐷 ≶ 0 es factorizable sobre R
• si D es cuadrado perfecto (2𝑎𝑥 + 𝑏)2
−𝐷 ≶ 0
es factorizable sobre Q.
• Teoremas:
1.- ∀𝑎 ∈ 𝑅: 𝑎2
≥ 0
2.- 𝑎. 𝑏 > 0 ↔ 𝑎 > 0 ∧ 𝑏 > 𝑜 ∨ (𝑎 < 0 ∧
𝑏 < 0)

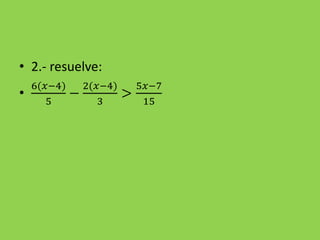
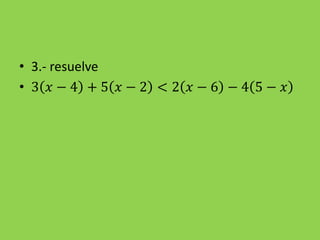
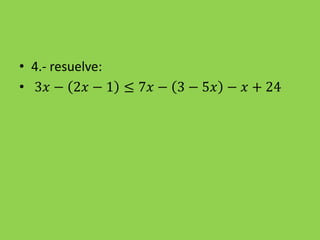
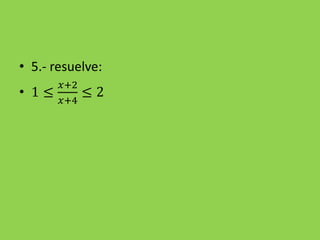
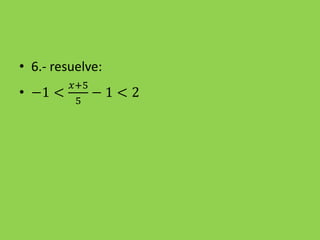
15. 3.- 𝑎. 𝑏 < 0 ↔ [ 𝑎 > 0 ∧ 𝑏 < 0 ∨ 𝑎 < 0 ∧ 𝑏 > 0 ]
4.- 𝑠𝑒𝑎𝑛 𝑥 ≥ 0 ∧ 𝑦 ≥ 0, 𝑙𝑢𝑒𝑔𝑜 𝑥2 > 𝑦2 ↔ 𝑥 > 𝑦
5.- ∀𝑎 > 0, 𝑥2 < 𝑎 ↔ − 𝑎 < 𝑥 < 𝑎

16. Puntos críticos
𝑃 𝑥 = 𝑎𝑥2
+ 𝑏𝑥 + 𝑐 ≶ 0
𝐷 > 0
Halla el CS de :
2𝑥2
− 7𝑥 + 3x > 0

17. II.- segundo caso (D=0)
I.- 2𝑎𝑥 + 𝑏 2 > 0
𝐶. 𝑆 = 𝑅 −
𝑏
2𝑎
II.- 2𝑎𝑥 + 𝑏 2 ≥ 0
𝐶𝑆 = 𝑅
III.- 2𝑎𝑥 + 𝑏 2 < 0
𝐶𝑆 ≠ 𝑅
IV.- 2𝑎𝑥 + 𝑏 2 ≤ 0
𝐶𝑆 = −
𝑏
2𝑎

18. III.- 𝑡𝑒𝑟𝑐𝑒𝑟 𝑐𝑎𝑠𝑜: 𝐷 < 0
I) 2𝑎𝑥 + 𝑏 2
− 𝐷 > 0
𝐶𝑆 = 𝑅
II) 2𝑎𝑥 + 𝑏 2
− 𝐷 ≥ 0
𝐶𝑆 = 𝑅
III) 2𝑎𝑥 + 𝑏 2
− 𝐷 < 0
𝐶𝑆 = ∅
IV) 2𝑎𝑥 + 𝑏 2
− 𝐷 ≤ 0
𝐶𝑆 = −∅

19. Resuelva:
𝑥 − 3 𝑥 − 2 + 𝑥 > −1

20. Pagina 28
1.- 𝑥2
− 5x + 4 < 0

21. 2.- 4𝑥2
+ 12𝑥 + 9 > 0

22. 3.- 𝑥2
− 4𝑥 > 0

23. 4.- 𝑥2
− 6𝑥 + 9 ≤ 0

24. 5.- 𝑥2
− 3𝑥 − 2 ≥ 0

25. 6.- 𝑥 + 3 2
− 𝑥 − 1 2
> 𝑥 − 2 2
+ 44

26. Pagina 29
7.- 𝑥2
− 4𝑥 − 5 > 0

27. 8.- 2𝑥2
− 11𝑥 + 12 ≤ 0

28. 9.- 𝑥2
− 16𝑥 + 64 ≤ 0

29. 10.- 𝑥2
+ 𝑥 − 3 𝑥 − 2 > 2

30. 11- ¿ para cuantos valores enteros de “n” el CS,
de la inecuación 𝑥2
− 𝑛𝑥 + 4 > 0 es todo los
reales?

31. 12.- 𝑥2
− 2𝑥 + 5 > 0

32. Trabajo grupal
1. 3𝑥2
− 10𝑥 + 3 > 0
2. Si 𝑥 ∈< 2; 4 > ¿ 𝑎 𝑞𝑢𝑒 𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝑜 𝑝𝑒𝑟𝑡𝑒𝑛𝑒𝑐𝑒 𝐸?
𝐸 =
4𝑥 − 6
2
3. Si 𝑥 ∈ 2; 5 calcula la suma del menor y mayor
valor que pude tomar 𝑃 =
𝑥+10
10
4. Calcula la suma de todos los valores enteros
positivos de x que satisfacen la inecuación
4𝑥 − 3 2
≤ 169

33. 5. ¿Cuántos valores enteros de x satisfacen el
siguiente sistema ?
𝑥
3
< 𝑥 − 6
𝑥
4
> 𝑥 − 5