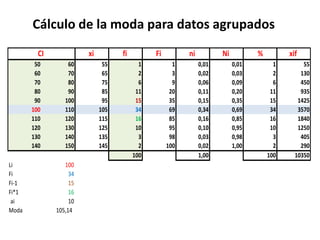
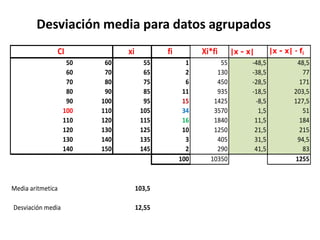
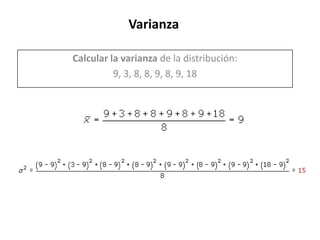
La mediana es el valor central de una distribución ordenada de menor a mayor. Se representa por Me y se puede calcular para variables cuantitativas. La moda es el valor con mayor frecuencia absoluta y se representa por Mo. La varianza es la media de los cuadrados de las desviaciones respecto a la media y se representa por σ2, mientras que la desviación estándar es la raíz cuadrada de la varianza y se representa por σ.