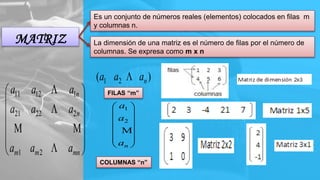
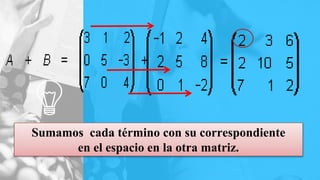
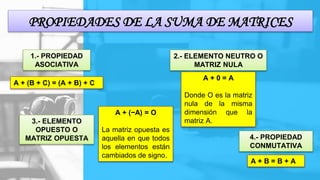
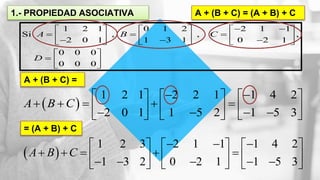
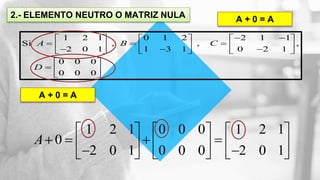
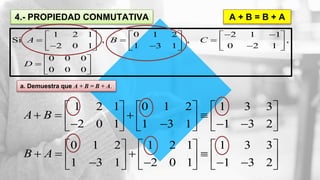
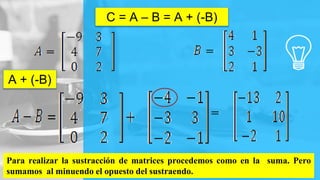
El documento explica las operaciones de suma y resta de matrices, indicando que deben tener la misma dimensión para poder realizar estas operaciones. Se presentan propiedades fundamentales como la conmutatividad, la asociatividad y la existencia de elementos neutros y opuestos. También se incluye un ejemplo práctico de suma y resta de matrices para ilustrar los conceptos discutidos.

1. OPERACIONES CON
MATRICES
(SUMA Y RESTA)

2. MATRIZ
COLUMNAS “n”
FILAS “m”












na
a
a

2
1
)( 21 naaa 
Es un conjunto de números reales (elementos) colocados en filas m
y columnas n.
La dimensión de una matriz es el número de filas por el número de
columnas. Se expresa como m x n












mnmm
n
n
aaa
aaa
aaa




21
22221
11211

3. SUMA Y RESTA DE MATRICES CON
PROPIEDADES
Para poder sumar o restar matrices, éstas deben tener el
mismo número de filas y de columnas. Es decir, si una matriz
es de orden 3 × 2 y otra de 3 × 3, no se pueden sumar ni
restar.
A + B = C
A - B = C

4. SUMA
Ejemplo:
Para la suma o adición de matrices deben tener la misma dimensión,
por ende se obtiene otra matriz de la misma dimensión.

5. Sumamos cada término con su correspondiente
en el espacio en la otra matriz.

6. PROPIEDADES DE LA SUMA DE MATRICES
4.- PROPIEDAD
CONMUTATIVA
2.- ELEMENTO NEUTRO O
MATRIZ NULA
A + (B + C) = (A + B) + C
3.- ELEMENTO
OPUESTO O
MATRIZ OPUESTA
1.- PROPIEDAD
ASOCIATIVA
A + 0 = A
Donde O es la matriz
nula de la misma
dimensión que la
matriz A.
A + (−A) = O
La matriz opuesta es
aquella en que todos
los elementos están
cambiados de signo.
A + B = B + A

7. 1.- PROPIEDAD ASOCIATIVA A + (B + C) = (A + B) + C
A + (B + C) =
= (A + B) + C
1 2 1 0 1 2 2 1 1
Si , , ,
2 0 1 1 3 1 0 2 1
0 0 0
0 0 0
A B C
D
      
              
 
  
 
 
1 2 1 2 2 1 1 4 2
2 0 1 1 5 2 1 5 3
A B C
      
                 
 
1 2 3 2 1 1 1 4 2
1 3 2 0 2 1 1 5 3
A B C
       
                  

8. 2.- ELEMENTO NEUTRO O MATRIZ NULA A + 0 = A
1 2 1 0 1 2 2 1 1
Si , , ,
2 0 1 1 3 1 0 2 1
0 0 0
0 0 0
A B C
D
      
              
 
  
 
A + 0 = A
1 2 1 0 0 0 1 2 1
0
2 0 1 0 0 0 2 0 1
A
     
              

9. 3.- ELEMENTO OPUESTO
O MATRIZ OPUESTA
A + (−A) = O
La matriz opuesta es aquella en que todos
los elementos están cambiados de signo.
1 2 1 0 1 2 2 1 1
Si , , ,
2 0 1 1 3 1 0 2 1
0 0 0
0 0 0
A B C
D
      
              
 
  
 
A + (−A) = O

10. 4.- PROPIEDAD CONMUTATIVA A + B = B + A
1 2 1 0 1 2 2 1 1
Si , , ,
2 0 1 1 3 1 0 2 1
0 0 0
0 0 0
A B C
D
      
              
 
  
 
a. Demuestra que A + B = B + A.
1 2 1 0 1 2 1 3 3
2 0 1 1 3 1 1 3 2
A B
     
                
0 1 2 1 2 1 1 3 3
1 3 1 2 0 1 1 3 2
B A
     
                

11. RESTA O SUSTRACCIÓN
Para la resta o sustracción de matrices, deben tener la misma
dimensión, por ende se obtiene otra matriz de la misma dimensión.
Si A y B, entonces la diferencia de A y B, que se denota por :
C = A – B = A + (-B)
A - B es una matriz C, tal que C es la suma de la matriz A y la
negativa de B, es decir:

12. C = A – B = A + (-B)
A + (-B)
Para realizar la sustracción de matrices procedemos como en la suma. Pero
sumamos al minuendo el opuesto del sustraendo.

13. Ejemplo

14. FÍN
Linografías:
http://www.ditutor.com/matrices/matriz.html
http://www.vadenumeros.es/segundo/tipos-y-producto-de-matrices.htm
http://www.lemat.unican.es/lemat/proyecto_lemat/matrices/nivel1/teoria/matrices17.htm
http://slideplayer.es/slide/94229/