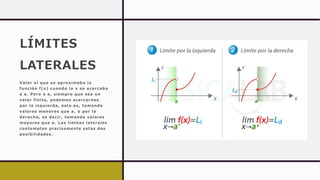
Este documento trata sobre funciones y conceptos básicos de cálculo diferencial. Explica que una función es una regla de correspondencia entre dos conjuntos donde a cada elemento del primer conjunto se le asigna un único elemento del segundo conjunto. También define conceptos como dominio, contradominio, variables independientes y dependientes, y métodos para representar funciones como diagramas sagitales y sistemas de coordenadas.

1. CÁLCULO
DIFERENCIAL
ELEMENTO DE
COMPETENCIA I

2. FUNCIONES
Una función f es una regla que asigna a
cada elemento x de un conjunto D
exactamente un elemento, llamado f(x),
de un conjunto
Una función es una regla de
correspondencia entre dos conjuntos de
tal manera que a cada elemento del
primer conjunto le corresponde uno y sólo
un elemento del segundo conjunto.
Al primer conjunto
(el conjunto D) se
le da el nombre de
dominio.
Al segundo
conjunto (el
conjunto C) se le
da el nombre de
contradominio o
imágen.

3. Una función se puede concebir también como un
aparato de cálculo. La entrada es el dominio, los
cálculos que haga el aparato con la entrada son en
sí la función y la salida sería el contradominio.
Esta forma de concebir la función facilita el
encontrar su dominio.

4. VIDEO DE APOYO

5. EJERCICIO
Representar la siguiente función:

6. REPRESENTACIÓN DE FUNCIONES
DIAGRAMA SAGITAL
Un diagrama llamado sagital, es la representación de dos
conjuntos, por
ejemplo, A y B que relacionan con flechas cada elemento de
A (preimagen), con su
respectiva imagen en B. Se indica en la parte superior la
relación de A en B con una flecha
curva.
Ejemplo:
Sea una función f definida por; f = {(2,c), (3,a), (4,d)

7. SISTEMA DE COORDENADAS O
CARTESIANO
Las ecuaciones dadas para
determinar una función, siempre
tendrán dos incógnitas.
Donde x será la variable
independiente (preimágen) e y
será la variable dependiente
(imagen).
Por lo tanto, f (x) = y. Entonces,
para obtener los puntos deben
reemplazarse los valores de x en
la función y resolver.
Es útil anotar estos datos en una
tabla con los valores para x e y.

8. EJEMPLO
Representar en el sistema cartesiano una función real f, donde
f (x) = x + 1.
Si se reemplazan los valores de x en la función:
- f (1) = 1 + 1 = 2
- f (2) = 2 + 1 = 3
- f (3) = 3 + 1 = 4
- f (- 1) = - 1 + 1 = 0
- f (- 2) = - 2 + 1 = - 1
Se obtienen las coordenadas (1,2) (2,3) (3,4) ( -1,0) (-2,-1).

9. VIDEO DE
APOYO

10. EJERCICIO
Representar la siguiente función en un
sistema de coordenadas.

11. DOMINIO Y RANGO
Para encontrar el dominio y el rango a partir de la representación
gráfica de una función, hay
que observar la proyección de ésta sobre el eje de coordenadas.
Como ya es sabido, los valores
del dominio se expresan en eje de las abscisas (eje x), y el recorrido
en el eje de las ordenadas
(eje y).

12. EJEMPLO
D e t e r m i n a r e l d o m i n i o y e l r a n g o d e l a f u n c i ó n a p a r t i r d e s u g r á f i c a .
S e p u e d e o b s e r v a r q u e t o d o s l o s v a l o r e s d e l a v a r i a b l e i n d e p e n d i e n t e x ,
s o n t o d o s l o s n ú m e r o s
r e a l e s e n t r e e l – 3 y e l 3 , y l o s v a l o r e s q u e t o m a l a v a r i a b l e i n d e p e n d i e n t e
y s o n l o s n ú m e r o s
r e a l e s e n t r e e l 0 y 9 .
E n t o n c e s :
- E l d o m i n i o d e f c o r r e s p o n d e a ; D o m ( f ) = i n t e r v a l o [ - 3 , 3 ]
- E l r a n g o c o r r e s p o n d e a ; R a n g o ( f ) = i n t e r v a l o [ 0 , 9 ]

13. VIDEO DE
APOYO

14. EJERCICIO
Determina el dominio y rango de la
función mediante la siguiente gráfica:

15. VARIABLES
DEPENDIENTES E
INDEPENDIENTES

16. VARIABLES
INDEPENDIENTES
Un variable independiente es una variable
que representa una cantidad que se
modifica en un experimento.
A menudo x es la variable que se utiliza
para representar la variable independiente
en una ecuación.
Ejemplo:
Estás haciendo tareas domésticos para
ganar tu mesada. Por cada tarea que haces
obtienes $3
¿Cuál es la variable independiente?
La variable independiente es la cantidad de
tareas que haces, pues esta es la variable
sobre la que tienes control.

17. VARIABLES
DEPENDIENTES
Una variable dependiente representa una
cantidad cuyo valor depende de cómo se modifica
la variable independiente.
A menudo y es la variable que se utiliza para
representar la variable dependiente en una
ecuación.
Ejemplo:
Utilicemos el mismo contexto.
Estás haciendo tareas domésticas para ganar tu
mesada. Por cada tarea que haces obtienes $3
¿Cuál es la variable dependiente?
La variable dependiente es la cantidad de dinero
que obtienes, pues la cantidad de dinero que
ganas depende del número de tareas que hagas.

18. VIDEO DE APOYO

19. EJERCICIO
Compras cajas de galletas en una panadería. Cada caja de galletas cuesta $4.
¿Cuáles de las siguientes proposiciones son verdaderas?
• La variable dependiente es el número de cajas de galletas que compras.
• La variable independiente es el número de cajas de galletas que compras.
• La variable dependiente es la cantidad de dinero que gastas en galletas.
• La variable independiente es la cantidad de dinero que gastas en galletas.

20. Vas a correr. Por cada milla que corres, quemas 100 calorías.
¿Cuáles de las siguientes proposiciones son verdaderas?
• La variable dependiente es el número de millas que corres.
• La variable dependiente es la cantidad de calorías que quemas.
• La variable independiente es el número de millas que corres.
• La variable independiente es la cantidad de calorías que quemas

21. FUNCIONES SECCIONALMENTE DEFINIDAS
Una función definida por partes es aquella que no esta definida por
una ecuación sola, sino por dos o más. Cada ecuación es válida para
algún intervalo .

22. EJEMPLOS
Ejemplo 1:
Considere la función definida como sigue.
Las funciones definidas por partes también pueden tener
discontinuidades ("saltos"). La función en el ejemplo
siguiente tiene discontinuidades en y

23. Ejemplo 2:
Grafique la función definida como se muestra.

24. VIDEO DE APOYO

25. FUNCIONES
CRECIENTES Y
DECRECIENTES
FUNCIÓN CRECIENTE
Diremos que una función es creciente
cuando a medida que crece el valor de la
variable independiente crece el valor de la
función.
FUNCIÓN DECRECIENTE
Diremos que una función es decreciente
cuando a medida que el valor de la
variable independiente aumenta el valor
de la función disminuye.

26. VIDEO DE
APOYO

27. EJERCICIO
Determine si las siguientes funciones
graficadas son crecientes o decrecientes:

28. MODELO DE
FUNCIONES
Un Modelo Lineal usa una función lineal (de
forma y=mx+b ) para modelar una
situación de cambio constante, ya sea de
crecimiento o decrecimiento.

29. EJEMPLO
Ejemplo 1
Estás en el techo de un edificio de 20 pies de alto. Tiras una
pelota al aire con una velocidad vertical inicial de 40 pies por
segundo, de manera que caiga en piso y no en el techo. ¿Cuán
alto llegará la pelota? ¿En qué punto alcanzará su altura
máxima? ¿Cuándo llegará al piso la pelota?
Solución:
Esta situación puede ser modelada por una función cuadrática
de forma h(t)=−16t2+v0t+h0 donde h(t) representa la altura
sobre el piso y:
la constante -16 (en unidades de ft/sec2 ) se obtiene de la
fuerza de gravedad hacia abajo;
t representa el tiempo (en segundos) desde que la pelota fue
lanzada;
v0 representa la velocidad inicial (es pies/ seg) de la pelota
h0 representa la altura inicial (en pies) de la pelota.
Podemos escribir la función como h(t)=−16t2+40t+20 .

30. VIDEO DE APOYO

31. LIMITE DE
UNA
FUNCIÓN
Un límite es una magnitud fija a la que se
aproximan cada vez más los términos de
una secuencia infinita de magnitudes.

32. EJEMPLO
Determina los límites de las siguientes funciones:

33. VIDEO DE
APOYO

34. LÍMITES
LATERALES
Valor al que se aproximaba la
función f(x) cuando la x se acercaba
a a. Pero a a, siempre que sea un
valor finito, podemos acercarnos
por la izquierda, esto es, tomando
valores menores que a, o por la
derecha, es decir, tomando valores
mayores que a. Los límites laterales
contemplan precisamente estas dos
posibilidades.

35. EJEMPLOS
Consideremos la función f(x)=1/x y que
queremos calcular su límite en 0, es decir,
el límite
Cuando x toma valores cercanos a 0 por
su derecha, f(x) toma valores positivos
grandes:
Deducimos que el límite de f(x) cuando x
tiende a 0 por la derecha es infinito
positivo:

36. Por tanto, el límite de f(x) cuando x tiende a 0 por la
izquierda es infinito negativo:
Gráfica de la función:

37. VIDEO DE APOYO

38. LIMITE
INFINITO
Existe límite infinito cuando la función f(x)
llega a valores que crecen continuamente,
es decir que se puede hacer la función tan
grande como queramos. ... Se dice entonces
que f(x) diverge a infinito. Esto puede
ocurrir cuando la variable x tienda a un
valor finito a o también cuando x tienda al
infinito

39. EJEMPLO
Indicar si existe el siguiente límite:
Si graficamos la función:

40. VIDEO DE
APOYO

41. CONTINUIDAD
Una función es continua si su gráfica puede
dibujarse de un solo trazo.
Se dice que la función es discontinua si no
es continua, es decir, presenta algún punto
en el que existe un salto y la gráfica se
rompe.

42. EJEMPLOS
La continuidad lateral de una función f
estudia si ésta es continua en los
laterales de un punto x=a. Por lo tanto,
se estudia la continuidad lateral a
izquierda o derecha.

43. VIDEO DE
APOYO