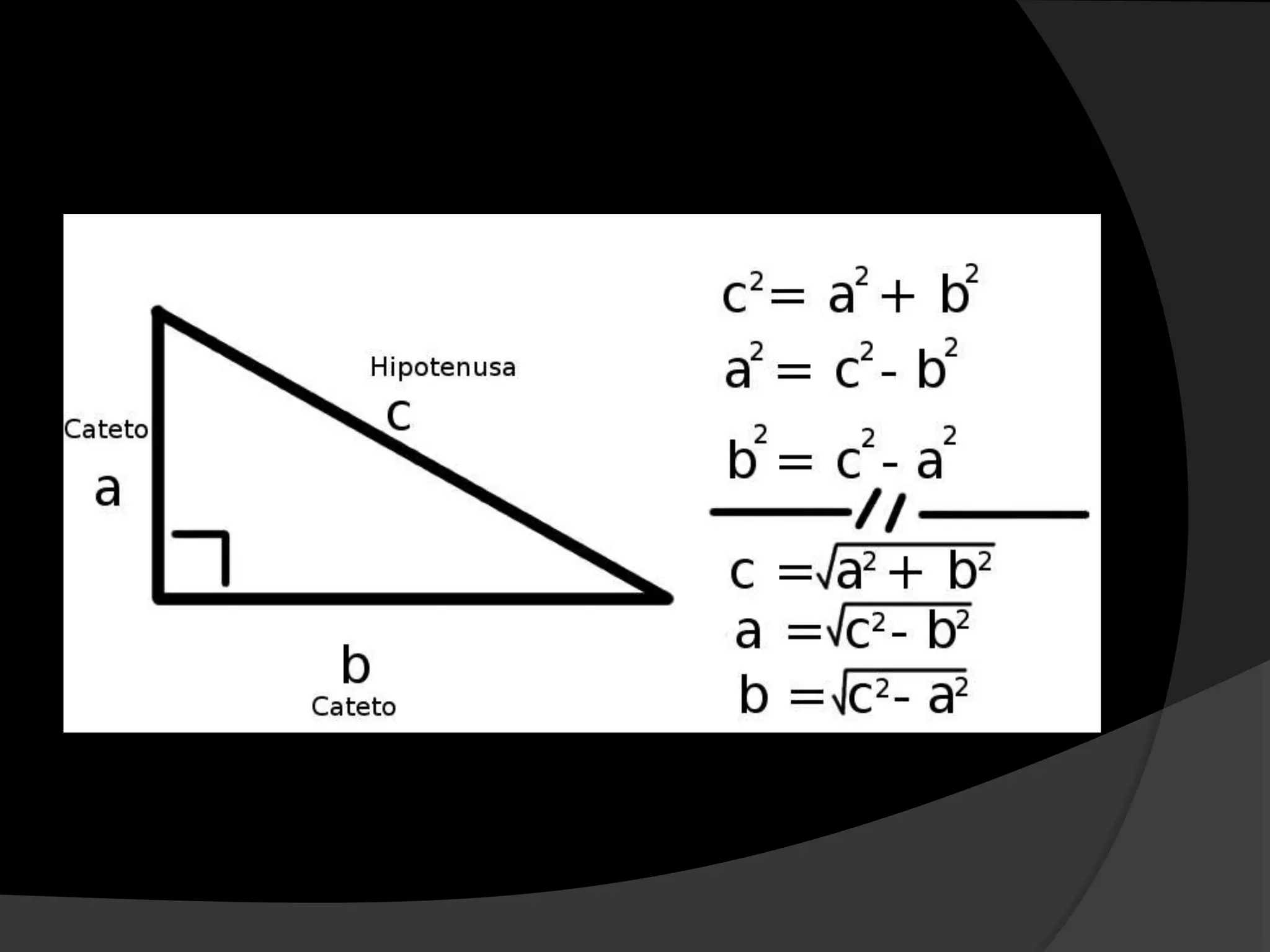
Pitágoras de Samos (569 a.C. – 475 a.C.) fue un filósofo y matemático griego, conocido como el primer matemático puro y fundador de la hermandad pitagórica, que se interesaba en diversas disciplinas además de la matemática. Su célebre teorema, que establece que en un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos, tiene aplicaciones prácticas en arquitectura, navegación y criminología. A pesar de la escasez de documentos sobre su vida, su influencia se considera significativa tanto en matemáticas como en pensamiento religioso y filosófico.