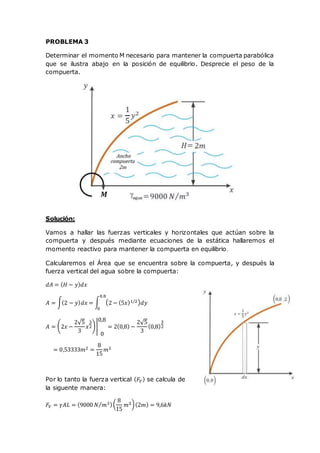
Este documento describe cómo calcular el momento necesario (M) para mantener una compuerta parabólica en equilibrio. Se calcula el área sobre la compuerta, la fuerza vertical del agua (FV), el centro de presión vertical (xCP) y la fuerza horizontal (FH). Luego, usando las ecuaciones de equilibrio estático, se determina que el momento requerido (M) es de 26,304 kN-m.

1. PROBLEMA 3
Determinar el momento M necesario para mantener la compuerta parabólica
que se ilustra abajo en la posición de equilibrio. Desprecie el peso de la
compuerta.
Solución:
Vamos a hallar las fuerzas verticales y horizontales que actúan sobre la
compuerta y después mediante ecuaciones de la estática hallaremos el
momento reactivo para mantener la compuerta en equilibrio.
Calcularemos el Área que se encuentra sobre la compuerta, y después la
fuerza vertical del agua sobre la compuerta:
𝑑𝐴 = ( 𝐻 − 𝑦) 𝑑𝑥
𝐴 = ∫(2 − 𝑦) 𝑑𝑥 = ∫ (2 − (5𝑥)1/2) 𝑑𝑦
0,8
0
𝐴 = (2𝑥 −
2√5
3
𝑥
3
2)|
0,8
0
= 2(0,8) −
2√5
3
(0,8)
3
2
= 0,53333𝑚2 =
8
15
𝑚2
Por lo tanto la fuerza vertical ( 𝐹𝑉) se calcula de
la siguente manera:
𝐹𝑉 = 𝛾𝐴𝐿 = (9000 𝑁 𝑚3⁄ )(
8
15
𝑚2)(2𝑚) = 9,6𝑘𝑁

2. Ahora procederemos a calcular el centro de presión de la sección donde
actúan las fuerzas:
𝑥 𝑐𝑝 =
𝛾𝑙 ∫ 𝑥𝑑𝐴
0,8
0
𝐹𝑉
=
𝛾𝑙
𝐹𝑉
∫ 𝑥(2 − 𝑦) 𝑑𝑥
0,8
0
=
𝛾𝑙
𝐹𝑉
∫ 𝑥 (2 − (5𝑥)
1
2) 𝑑𝑥
0,8
0
=
𝛾𝑙
𝐹𝑉
(2(
1
2
𝑥2) −
2√5
5
𝑥
5
2)|
0,8
0
=
(9 𝑘𝑁 𝑚3⁄ )(2𝑚)
9,6𝑘𝑁
[(0,8)2 −
2√5
5
(0,8)
5
2]= 0,24𝑚
Ahora calcularemos la Fuerza Horizontal ( 𝐹𝐻) con respecto al área
proyectada, con lo cual:
𝐹𝐻 = 𝛾ℎ 𝑐𝑔 𝐴 = (9000 𝑁 𝑚3⁄ )(1𝑚)(2𝑚)(2𝑚) = 36𝑘𝑁
El valor del centro de presión para la fuerza horizontal (ycp), se calcula de
acuerdo al área proyectada desde la superficie, por lo cual:
𝑦𝑐𝑝 = ℎ 𝑐𝑔 +
𝐼𝑐𝑔
𝐴 ∙ ℎ 𝑐𝑔
= 1𝑚 +
1
12
(2𝑚)(2𝑚)3 sin2 90°
[(2𝑚)(2𝑚)](1𝑚)
=
1
3
𝑚
𝑦 = 𝐻 − 𝑦𝑐𝑝 = 2𝑚 −
1
3
𝑚 =
2
3
𝑚
Por lo cual, el momento con respecto a la bisagra de la compuerta será:
+↻ ∑( 𝑀) 𝑂 = 0
𝑀 − (
2
3
𝑚)(36𝑘𝑁) − (0,24𝑚)(9,6𝑘𝑁) = 0
𝑴 = 𝟐𝟔, 𝟑𝟎𝟒𝒌𝑵 ∙ 𝒎