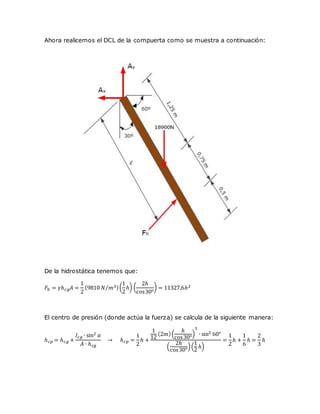
El documento trata sobre el problema de una compuerta sumergida en un canal que se abre a un nivel específico del agua. Se detalla el proceso de cálculo para determinar la altura h en la que la compuerta comienza a abrirse, utilizando principios de mecánica de fluidos y leyes de equilibrio. Los resultados indican que la compuerta comienza a abrirse a una altura de 0,8 m.

1. Problema de Placas Planas Sumergidas (Mecánica de Fluidos)
Un fluido está contenido en un canal por una compuerta uniforme de 2,5𝑚 de
longitud sujeta por una bisagra en 𝐴. si la compuerta está diseñada para
abrirse cuendo el nivel del agua es h como se muestra en la figura.
Si el ancho de la compuerta es de 6,56𝑓𝑡, determine la altura h, si el peso de la
compuerta es de 4,2𝑘𝑙𝑏.
La gravedad específica del fluido es 1
Solución:
Pasamos todas las unidades al sistema internacional como se muestra a
continuación:
𝑊 = 4200𝑙𝑏 ×
4,45𝑁
1𝑙𝑏
= 18690𝑁
𝑏 = 6,56𝑓𝑡 ×
12𝑖𝑛
1𝑓𝑡
×
25,4𝑚𝑚
1 𝑖𝑛
×
1𝑚
1000𝑚𝑚
= 1,9994𝑚 ≈ 2𝑚
El área en el cual actua el fluido se halla de la siguiente manera:
𝐴 = 𝑏𝑎𝑠𝑒 × 𝑎𝑙𝑡𝑢𝑟𝑎 = (2𝑚)(
ℎ
cos30
) =
2ℎ
cos30°

2. Ahora realicemos el DCL de la compuerta como se muestra a continuación:
De la hidrostática tenemos que:
𝐹ℎ = 𝛾ℎ 𝑐𝑔 𝐴 =
1
2
(9810 𝑁 𝑚3⁄ )(
1
2
ℎ) (
2ℎ
cos30°
) = 11327,6ℎ2
El centro de presión (donde actúa la fuerza) se calcula de la siguiente manera:
ℎ 𝑐𝑝 = ℎ 𝑐𝑔 +
𝐼𝑐𝑔 ∙ sin2 𝛼
𝐴 ∙ ℎ 𝑐𝑔
→ ℎ 𝑐𝑝 =
1
2
ℎ +
1
12
(2𝑚)(
ℎ
cos30°
)
3
∙ sin2 60°
(
2ℎ
cos30°
)(
1
2
ℎ)
=
1
2
ℎ +
1
6
ℎ =
2
3
ℎ

3. Area de la compuerta afectada por la presión del agua
Pero:
ℎ 𝑐𝑝 = 𝐿 𝑝 cos30° → 𝐿 𝑝 =
ℎ 𝑐𝑝
cos30°
=
2ℎ
3 cos30°
De la figura de la sección de la compuerta afectada por el agua tenemos la
siguiente relación:
ℎ = 𝐿∗ cos30° → 𝐿∗ =
ℎ
cos30°
por lo tanto, la distancia desde la bisagra A hasta el punto donde actua la
fuerza hidrostática se calcula asi:
2𝑚 = 𝐿 − 𝐿 𝑝 + 𝐿∗ → 𝐿 = 2𝑚 − 𝐿∗ + 𝐿 𝑝
Reemplazando valores, tenemos que:
𝐿 = 2𝑚 −
ℎ
cos30°
+
2ℎ
3 cos30°
= 2 −
1
3
(
ℎ
cos30°
)

4. Ahora del DCL de la compuerta, haciendo uso de las ecuaciones de equilibrio,
tenemos que:
↺ ∑𝑀𝐴 = 0
(18690𝑁)(1,25 sin 30° 𝑚) − (11327,6ℎ2)(2 −
1
3
(
ℎ
cos30°
)) = 0
Realizamos las operaciones y nos queda:
0,385ℎ3 − 2ℎ2 +
11681,25
11327,6
= 0 → 0,385ℎ3 − 2ℎ2 + 1,0312 = 0
Despejando ℎ3 e iterando tenemos que:
ℎ3 − 5,2ℎ2 + 2,8 = 0
𝒉 2 1 0,9 0,8 0,7 0,6
𝒇(𝒉) −10 −1,4 −0,683 −0,016 0,595 1,144
Podemos decir que cuando 𝒉 = 𝟎, 𝟖𝒎 la compuerta comienza a abrir.