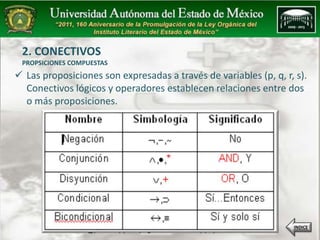
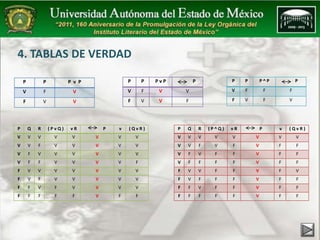
Este documento presenta un programa de estudio sobre matemáticas discretas para una licenciatura en informática administrativa. El programa cubre proposiciones lógicas, conectivos, operaciones lógicas y tablas de verdad. Incluye estrategias didácticas como exposición, elaboración de tarjetas y ejercicios. Finalmente, propone una práctica en un laboratorio de electrónica para aplicar los conceptos en circuitos.

1. PROGRAMA DE ESTUDIOS POR COMPETENCIAS
MATEMATICAS DISCRETAS
PROGRAMA EDUCATIVO: LICENCIADO EN INFORMÁTICA ADMINISTRATIVA
AREA DE DOCENCIA: INFORMÁTICA
CREDITOS: 8
AUTOR: ING. SONIA GUADALUPE MORALES MARTINEZ

2. PROPOSICIONES LÓGICAS
PROPOSITO DEL TEMA
Identificar las operaciones básicas de las proposiciones lógicas con los conectores y
resolver ejercicios utilizando las tablas de verdad que sirven para estimar los valores
de verdad de expresiones lógicas.
CONOCIMIENTOS
 Proposiciones
 Conectores
 Operaciones Lógicas
 Tablas de verdad

3. ESTRATEGIAS DIDACTICAS
 Exposición del maestro de los conceptos, tablas de verdad y conectores.
 Elaboración de tarjetas bibliográficas con las tablas de verdad de los
conectores básicos.
 Explicación de algunos ejemplos con tablas de verdad.
 Ejercicios extra clase.
 Realizar una práctica sencilla, de la aplicación de la lógica proposicional en los
circuitos computacionales.

4. 1. PROPOSICIONES
 Sentencias declarativa, o reglas las cuales
tienen valores de verdad.
 Valores, verdadero o falso. Pero no ambos
(verdadero y falso) y tampoco pueden no
tomar ningún valor.
 Una proposición es un hecho.
 Los argumentos de las proposiciones son:
premisas y conclusiones de una proposición.
 Las proposiciones son portadoras de veracidad
y falsedad.

5. EJEMPLOS DE PROPOSICIONES LOGICAS VERDADERAS
 El cielo es azul
 La nieve es fría
 12*12=144
 Vicente Fox fue presidente de la Republica Mexicana
 La Segunda Guerra Mundial duro desde 1939 hasta 1945

6. EJEMPLOS DE PROPOSICIONES LOGICAS FALSAS
 Honda hace televisiones
 El General Fidel Castro es un Demócrata
 8+99=231
 Los Insectos crean su comida a través de fotosíntesis
INDICE

7. 2. CONECTIVOS
PROPSICIONES COMPUESTAS
 Las proposiciones son expresadas a través de variables (p, q, r, s).
Conectivos lógicos y operadores establecen relaciones entre dos
o más proposiciones.
INDICE

8. 3. OPERACIONES LÓGICAS
Negación
La negación es la inversa de los valores de verdad de una declaración
Ejemplos
Algunas personas tienen miedo a morir (p)
Algunas personas no tienen miedo a morir (p)

9. Conjunción
Cuando conjugamos dos declaraciones, tiene el sentido de afirmar
que son simultáneamente verdaderas.
p = Londres es capital de Inglaterra
q = Cuba es una isla
Londres es capital de Inglaterra y Cuba es una isla

10. Disyunción
La disyunción tiene la función de enlazar dos proposiciones,
indicando que al menos una de ellas es verdadera o ambas.
p = 3 es un número primo
q = 3 es un número natural
3 es un número primo o 3 es un número natural

11. Condicional
 Al relacionarse dos proposiciones con este conector es muy
importante distinguir la que queda a la izquierda (a la que se le
llama antecedente), de la que queda a la derecha (que se llama
consecuente).
 El sentido de este conector es señalar, que si la proposición
antecedente es verdadera, también lo es la proposición
consecuente.

12. Ejemplo:
p = Marte es un planeta
q = Marte brilla con luz propia
Si Marte es un planeta entonces Marte brilla con luz
propia

13. Bicondicional
Esta expresión es un conector lógico que al relacionar dos
proposiciones indica que el valor de verdad de ambas es el mismo,
ya sea verdadero o falso.
p = Febrero tiene 29 días
q = El año es bisiesto
Febrero tiene 29 días si y solo si el año es bisiesto

14. Ejemplo: (pq)(rq)
No variables=n
No prop=2 ⁿ

15. 4. TABLAS DE VERDAD
P P P v P
V F V
F V V
P P P v P P
V F V V
F V V F
P P P ^ P P
V F F F
F V F V
P Q R ( P v Q ) v R P v ( Q v R )
V V V V V V V V
V V F V V V V V
V F V V V V V V
V F F V V V V F
F V V V V V V V
F V F V V V V V
F F V F V V V V
F F F F F V F F
P Q R ( P ^ Q ) v R P v ( Q v R )
V V V V V V V V
V V F V F V F F
V F V F F V F F
V F F F F V F F
F V V F F V F V
F V F F F V F F
F F V F F V F F
F F F F F V F F

16. 5. TAUTOLOGÍA Y CONTRADICCIONES
Tautología: Son aquellas fórmulas que son ciertas para
cualquier valoración de los símbolos proposicionales que
contiene.
Contradicción: Son aquellas fórmulas que son falsas
para cualquier valoración de los símbolos proposicionales
que contiene.

17. PRACTICA EN EL LABORATORIO DE ELECTRÓNICA
La práctica es dirigida por un Profesor de Tiempo Completo del Centro Universitario (Dr. Rodolfo Zola García Lozano).
Material (recursos de los alumnos, organizados por equipos)

18. Desarrollo de la práctica
Experimento 1. Comprobar el funcionamiento de las compuertas lógicas.
Experimento 2. Comprobar dos funciones que se hacen con compuertas lógicas (un
sumador de dos bits)
Experimento 3. Comprobar la aplicación de las funciones para implementar circuitos de
aplicación (sumador de dos palabras de cuatro bits)

19. REFLEXIÓN FINAL
Durante la presentación podemos ver los tres momentos metódicos, durante la
apertura conocer las diferentes operaciones, términos y tablas de verdad, ya para
el desarrollo la solución de ejemplos y ejercicios con la supervisión del docente,
para que los alumnos sepan que están resolviendo correctamente, ya para el cierre
y conocer la aplicación de estos conocimientos matemáticos en la vida real, la
propuesta es la elaboración de una practica donde los alumnos pueden relacionar
lo aprendido con el mundo real.
Cabe mencionar que los alumnos son de tercer semestre y no han tenido ningún
acercamiento con materias como electrónica o sistemas digitales, sin embargo con
esta pequeña practica pueden ver donde son aplicados los conocimientos
adquiridos de lógica proposicional.

20. BIBLIOGRAFÍA
INDICE