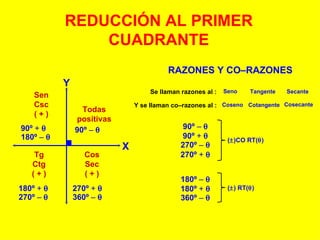
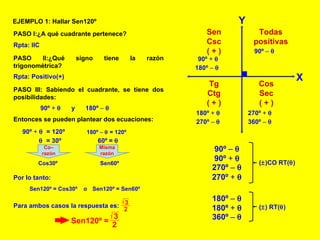
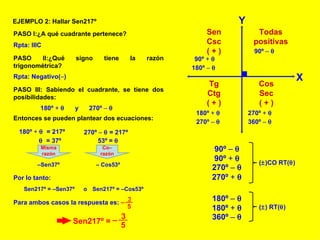
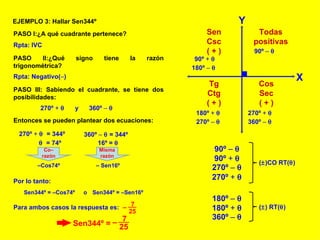
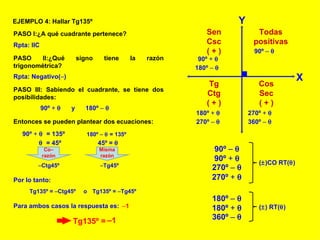
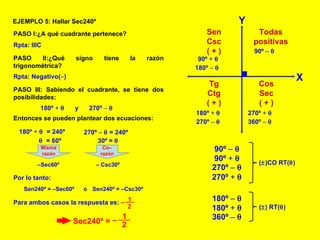
El documento explica cómo calcular las funciones trigonométricas en los cuadrantes del círculo trigonométrico. Define las razones y co-razones trigonométricas y muestra ejemplos de cómo calcular Sen, Tg, Sec, etc. para ángulos dados utilizando las propiedades de los cuadrantes.

1. REDUCCIÓN AL PRIMER CUADRANTE Todas positivas Sen Csc ( + ) Tg Ctg ( + ) Cos Sec ( + ) 90º –  90º +  180º –  180º +  270º –  270º +  360º –  RAZONES Y CO–RAZONES Se llaman razones al : Seno Tangente Secante Y se llaman co–razones al : Coseno Cotangente Cosecante (  )CO RT(  ) (  ) RT(  ) X Y 90º –  90º +  270º –  270º +  180º –  180º +  360º – 

2. EJEMPLO 1: Hallar Sen120º PASO I:¿A qué cuadrante pertenece? Rpta: IIC PASO II:¿Qué signo tiene la razón trigonométrica? Rpta: Positivo(+) PASO III: Sabiendo el cuadrante, se tiene dos posibilidades: 90º +  y 180º –  Entonces se pueden plantear dos ecuaciones: 90º +  = 120º 180º –  = 120º  = 30º 60º =  Co–razón Cos30º Sen60º Por lo tanto: Sen120º = Cos30º Sen120º = Sen60º o Para ambos casos la respuesta es: Misma razón X Y Todas positivas Sen Csc ( + ) Tg Ctg ( + ) Cos Sec ( + ) 90º –  90º +  180º –  180º +  270º –  270º +  360º –  (  )CO RT(  ) 90º –  90º +  270º –  270º +  (  ) RT(  ) 180º –  180º +  360º –  3 2 Sen120º = 3 2

3. EJEMPLO 2: Hallar Sen217º PASO I:¿A qué cuadrante pertenece? Rpta: IIIC PASO II:¿Qué signo tiene la razón trigonométrica? Rpta: Negativo( – ) PASO III: Sabiendo el cuadrante, se tiene dos posibilidades: 180º +  y 270º –  Entonces se pueden plantear dos ecuaciones: 180º +  = 217º 270º –  = 217º  = 37º 53º =  Misma razón – Sen37º – Cos53º Por lo tanto: Sen217º = –Sen37º Sen217º = –Cos53º o Para ambos casos la respuesta es: Co–razón X Y Todas positivas Sen Csc ( + ) Tg Ctg ( + ) Cos Sec ( + ) 90º –  90º +  180º –  180º +  270º –  270º +  360º –  (  )CO RT(  ) 90º –  90º +  270º –  270º +  (  ) RT(  ) 180º –  180º +  360º –  3 5 – 5 3 Sen217º = –

4. EJEMPLO 3: Hallar Sen344º PASO I:¿A qué cuadrante pertenece? Rpta: IVC PASO II:¿Qué signo tiene la razón trigonométrica? Rpta: Negativo( – ) PASO III: Sabiendo el cuadrante, se tiene dos posibilidades: 270º +  y 360º –  Entonces se pueden plantear dos ecuaciones: 270º +  = 344º 360º –  = 344º  = 74º 16º =  Co–razón – Cos74º – Sen16º Por lo tanto: Sen344º = –Cos74º Sen344º = –Sen16º o Para ambos casos la respuesta es: Misma razón X Y Todas positivas Sen Csc ( + ) Tg Ctg ( + ) Cos Sec ( + ) 90º –  90º +  180º –  180º +  270º –  270º +  360º –  (  )CO RT(  ) 90º –  90º +  270º –  270º +  (  ) RT(  ) 180º –  180º +  360º –  7 25 – 25 7 Sen344º = –

5. EJEMPLO 4: Hallar Tg135º PASO I:¿A qué cuadrante pertenece? Rpta: IIC PASO II:¿Qué signo tiene la razón trigonométrica? Rpta: Negativo( – ) PASO III: Sabiendo el cuadrante, se tiene dos posibilidades: 90º +  y 180º –  Entonces se pueden plantear dos ecuaciones: 90º +  = 135º 180º –  = 135º  = 45º 45º =  Co–razón – Ctg45º – Tg45º Por lo tanto: Tg135º = – Ctg45º Tg135º = – Tg45º o Para ambos casos la respuesta es: Misma razón – 1 X Y Todas positivas Sen Csc ( + ) Tg Ctg ( + ) Cos Sec ( + ) 90º –  90º +  180º –  180º +  270º –  270º +  360º –  (  )CO RT(  ) 90º –  90º +  270º –  270º +  (  ) RT(  ) 180º –  180º +  360º –  Tg135º = – 1

6. EJEMPLO 5: Hallar Sec240º PASO I:¿A qué cuadrante pertenece? Rpta: IIIC PASO II:¿Qué signo tiene la razón trigonométrica? Rpta: Negativo( – ) PASO III: Sabiendo el cuadrante, se tiene dos posibilidades: 180º +  y 270º –  Entonces se pueden plantear dos ecuaciones: 180º +  = 240º 270º –  = 240º  = 60º 30º =  Misma razón – Sec60º – Csc30º Por lo tanto: Sen240º = –Sec60º Sen240º = –Csc30º o Para ambos casos la respuesta es: Co–razón X Y Todas positivas Sen Csc ( + ) Tg Ctg ( + ) Cos Sec ( + ) 90º –  90º +  180º –  180º +  270º –  270º +  360º –  (  )CO RT(  ) 90º –  90º +  270º –  270º +  (  ) RT(  ) 180º –  180º +  360º –  1 2 – 2 1 Sec240º = –