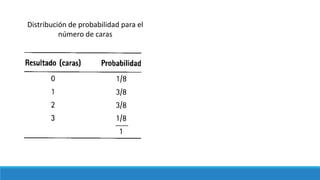
Este documento presenta conceptos básicos de estadística como variable aleatoria, distribución de probabilidad, función de masa de probabilidad, función de distribución acumulada, valor esperado y varianza. Explica que una variable aleatoria puede ser discreta o continua y que una distribución de probabilidad muestra los posibles resultados de un experimento aleatorio junto con sus probabilidades. Además, incluye un ejemplo de distribución de probabilidad para el número de caras obtenidas al lanzar una moneda tres veces.

1. Distribución de Probabilidad
ESTADÍSTICA I

2. Variable aleatoria
Es una variable cuyo valor es el resultado de un experimento
aleatorio a la cual se le puede asociar un número. Se denota por X.
Variable aleatoria discreta: Puede asumir solo ciertos valores, con frecuencia
números enteros y resulta principalmente del conteo.
Variable aleatoria continua: Resulta principalmente de la medición y puede
tomar cualquier valor, al menos dentro de un rango dado.

3. Distribución de probabilidad
Es un despliegue de todos los posibles resultados de un experimento junto con
las probabilidades de cada resultado.
Ejemplo:
𝜉 ={Lanzar una moneda tres veces y se anota el número de caras que se obtiene}

4. Distribución de probabilidad para el número de caras obtenidas en
tres lanzamientos de una moneda

5. Función de masa de probabilidad
La probabilidad de que la variable aleatoria X tome algún valor especifico, se
escribe:
𝑓 𝑥𝑖 = 𝑃 𝑋 = 𝑥𝑖
Por tanto la probabilidad de que los tres lanzamientos de una moneda resulten
en dos caras es:
𝑃 𝑋 = 2 =
3
8
.
Recordemos que :
0 ≤ 𝑃 𝑋 = 𝑥𝑖 ≤ 1
𝑃 𝑋 = 𝑥𝑖 = 1

6. Distribución de probabilidad para el
número de caras

7. Función de distribución acumulada
La función de distribución acumulada de una variable aleatoria discreta X,
denotada como 𝐹 𝑥 , es
𝐹 𝑥 = 𝑃 𝑋 ≤ 𝑥 =
𝑥 𝑖≤𝑥
𝑓(𝑥𝑖)
0 ≤ 𝐹 𝑥 ≤ 1

8. Valor esperado y varianza
La media o valor esperado de la variable aleatoria discreta X, denotada como 𝜇 o
𝐸(𝑋) es
La varianza de X, denotada como 𝜎2
o 𝑉(𝑋), es
La desviación estándar de X es 𝜎 = 𝑉 𝑋 1/2

9. Ejemplo
Distribución de probabilidad para el resultado
de lanzar un dado
𝜉 = {Lanzar un dado y observar el número de la cara superior}

10. Ejercicio
La siguiente es la tabla de probabilidades de que cierta computadora funcione
inadecuadamente 0, 1, 2, 3, 4, 5 o 6 veces en un día cualquiera. Basado en esta
tabla, calcule:
1. Probabilidad de que funcione inadecuadamente por lo menos tres veces
2. Probabilidad de que funcione inadecuadamente entre 1 y 4 veces inclusive
3. Valor esperado
4. Desviación estándar
Número de defectos 0 1 2 3 4 5 6
Probabilidad 0.17 0.29 0.27 0.16 0.07 0.03 0.01