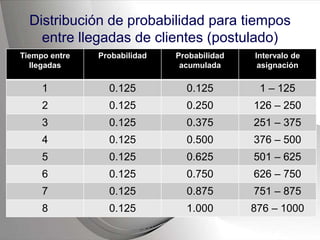
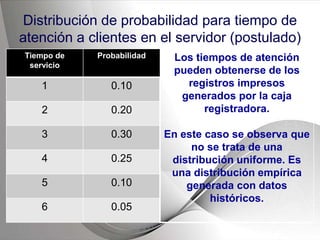
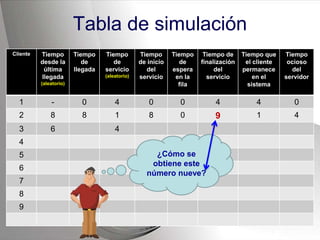
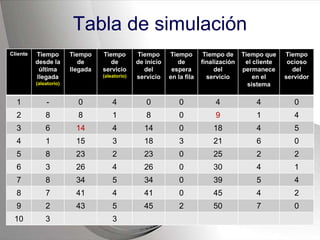
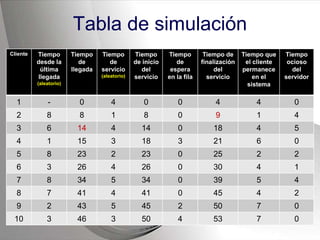
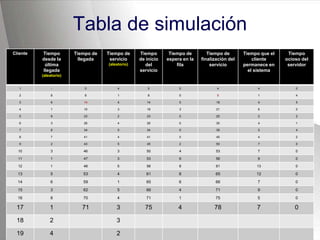
Este documento describe el proceso de simulación de sistemas. Explica qué es un sistema y una simulación, y proporciona un ejemplo de simulación de una fila de caja en un supermercado para determinar si se necesita instalar otra caja. Describe los pasos de definir los elementos del sistema, establecer postulados sobre los tiempos de llegada de clientes y atención, generar números aleatorios, y construir una tabla para simular el comportamiento del sistema durante 20 clientes.

1. Simulación de sistemas
G. Edgar Mata Ortiz

2. Contenido
• Sistema
• Simulación
• Ejemplo 1
• Análisis del ejemplo
• Datos, condiciones y postulados de la
simulación
• Realización de la simulación
• Análisis de resultados

3. ¿Quéesun
sistema?

4. Características de un sistema
• Elementos interrelacionados
• Interacción: Más que la suma de las
partes
• Propiedades emergentes
• Objetivo común
• Entradas
• Proceso
• Salidas

5. Simulación
• ¿Qué es simulación?
• Representación
• Imitación
Proceso
real comportamiento del
proceso
Postulados acerca del Modelado
y análisis

6. ¿Qué es simulación?
• La representación de la operación de un
sistema o proceso
• Se necesita desarrollar un conjunto de
postulados acerca de las relaciones entre
las entidades en estudio
• Con ello, es posible estimar el desempeño
del sistema con base en los datos
generados por la simulación

7. Ejemplo 1
• En un supermercado hay una sola caja, se
desea determinar si es necesario instalar
otra, con la finalidad de que la espera de
los clientes sea menor a 5 minutos y que
la fila nunca sea mayor a 6 personas.

8. Ejemplo 1
• Una sola caja
• Determinar si es necesario instalar
otra
• Con la finalidad de que:
–La espera de los clientes sea menor a 5
minutos
–Que la fila nunca sea mayor a 6
personas.

9. Ejemplo 1
• Una sola caja
• Determinar si es necesario instalar
otra

10. Ejemplo 1
• Con la finalidad de que:
–La espera de los clientes sea menor a 5
minutos
–Que la fila nunca sea mayor a 6
personas.

11. Ejemplo 1
• ¿Cuáles elementos van a ser analizados?
• ¿Qué datos son necesarios?
• ¿Qué postulados se van a establecer?
• Decidir el número de clientes o tiempo de
simulación
• Establecer el número de réplicas o
repeticiones de la simulación

12. Ejemplo 1
• ¿Cuáles elementos van a ser
analizados?
–Según la redacción del problema, se
necesita determinar el tiempo promedio
de espera en la fila y el número de
personas en la fila.

13. Ejemplo 1
• ¿Qué datos son necesarios?
–Además del tiempo promedio de espera
en la fila y el número de personas en la
fila se necesita:
–El tiempo entre llegadas de los clientes

14. Ejemplo 1
• ¿Qué postulados se van a
establecer?
–Con base en datos históricos podemos
postular el tiempo promedio de atención
al cliente
–También es necesario postular el
tiempo entre llegadas de los clientes

15. Ejemplo 1
• Condiciones de la simulación
–Se decide de acuerdo a las
necesidades
–Es necesario tomar en cuenta los
recursos necesarios y disponibles para
realizar la simulación
–Número de clientes o tiempo a simular
–Número de repeticiones o réplicas

16. Ejemplo 1 - Planteamiento
• Análisis de una fila para recibir un servicio
bajo las siguientes condiciones:
• Sólo hay un servidor
• Postulado de tiempo entre llegadas de
clientes
• Postulado acerca de tiempos de servicio
• Simular la llegada y atención de 20
clientes

17. Ejemplo 1 - Simulación
Proceso
real comportamiento del
proceso
Postulados acerca del Modelado
y análisis
Distribución de
probabilidad para tiempos
entre llegadas de clientes
(postulado):
Se postula una distribución
uniforme con tiempo
mínimo de 1 minuto y
máximo de 8 minutos
Distribución de
probabilidad para tiempos
de atención a cliente
(postulado):
Se postula una distribución
empírica con tiempo
mínimo de 1 minuto y
máximo de 6 minutos

18. Ejemplo 1 - Simulación
• Los tiempos
postulados toman
la forma de una
tabla de
distribución de
probabilidades,
como se muestra
en las diapositivas
siguientes

19. Distribución de probabilidad para tiempos
entre llegadas de clientes (postulado)
Tiempo entre
llegadas
Probabilidad Esta fase de la simulación
es muy importante,
generalmente se basa en
datos históricos.
Cuando no se dispone de
datos históricos se recure
a la experiencia e
intuición.
Y si no se tiene
experiencia, se postulan
las distribuciones más
sencillas o más comunes.
1 0.125
2 0.125
3 0.125
4 0.125
5 0.125
6 0.125
7 0.125
8 0.125

20. Distribución de probabilidad para tiempos
entre llegadas de clientes (postulado)
Tiempo entre
llegadas
Probabilidad Se agregan dos columnas
para calcular los intervalos
de asignación que simularán
las llegadas de los clientes
en tiempos aleatorios
basados en la distribución
postulada.
Observando la tabla de la
diapositiva siguiente, es
evidente su proceso de
construcción.
1 0.125
2 0.125
3 0.125
4 0.125
5 0.125
6 0.125
7 0.125
8 0.125

21. Distribución de probabilidad para tiempos
entre llegadas de clientes (postulado)
Tiempo entre
llegadas
Probabilidad Probabilidad
acumulada
Intervalo de
asignación
1 0.125 0.125 1 – 125
2 0.125 0.250 126 – 250
3 0.125 0.375 251 – 375
4 0.125 0.500 376 – 500
5 0.125 0.625 501 – 625
6 0.125 0.750 626 – 750
7 0.125 0.875 751 – 875
8 0.125 1.000 876 – 1000

22. Distribución de probabilidad para tiempo de
atención a clientes en el servidor (postulado)
Tiempo de
servicio
Probabilidad Los tiempos de atención
pueden obtenerse de los
registros impresos
generados por la caja
registradora.
En este caso se observa que
no se trata de una
distribución uniforme. Es
una distribución empírica
generada con datos
históricos.
1 0.10
2 0.20
3 0.30
4 0.25
5 0.10
6 0.05

23. Distribución de probabilidad para tiempo de
atención a clientes en el servidor (postulado)
Tiempo de
servicio
Probabilidad Se agregan dos columnas
para calcular los intervalos
de asignación que simularán
los tiempos aleatorios de
atención a clientes, basados
en la distribución postulada.
Observando la tabla de la
diapositiva siguiente, es
evidente su proceso de
construcción.
1 0.10
2 0.20
3 0.30
4 0.25
5 0.10
6 0.05

24. Distribución de probabilidad para tiempo de
atención a clientes en el servidor (postulado)
Tiempo de
servicio
Probabilidad Probabilidad
acumulada
Intervalo de
asignación
1 0.10 0.10 1 – 10
2 0.20 0.30 11 – 30
3 0.30 0.60 31 – 60
4 0.25 0.85 61 – 85
5 0.10 0.95 86 – 95
6 0.05 1.00 96 – 100

25. Ejemplo 1 – Realización de la
simulación
• Se enciende el cronómetro al llegar el primer
cliente.
• Este primer cliente no requiere tiempo entre
llegadas.
• Pero sí requiere determinar el tiempo de
atención.
• El tiempo de atención del primer cliente se
obtiene generando un número aleatorio entre 1
y 100.

26. Ejemplo 1 – Realización de la
simulación
• Digamos que se obtiene el número 73.
• Buscamos en los intervalos de asignación, en
cuál está ubicado el 73.
• Está entre 61 y 85, lo cuál se interpreta como
tiempo de atención de 4 minutos.
El 73, que se generó
aleatoriamente, está entre 61 y 85,
por lo tanto, el tiempo de
atención para el cliente número 1,
es de 4 minutos

27. Tabla de simulación
Cliente Tiempo
desde la
última
llegada
(aleatorio)
Tiempo
de
llegada
Tiempo
de
servicio
(aleatorio)
Tiempo
de inicio
del
servicio
Tiempo
de
espera
en la
fila
Tiempo de
finalización
del
servicio
Tiempo que
el cliente
permanece
en el
sistema
Tiempo
ocioso
del
servidor
1 - 0 4 0 0 4 4 0
2
3
4
5
6
7
8
9

28. Ejemplo 1 – Realización de la
simulación
• Para el segundo cliente, sí es necesario generar
aleatoriamente el tiempo entre llegadas.
• También se genera aleatoriamente el tiempo de
atención para el segundo cliente.
• Es sencillo comprender cómo se construye el
resto de la tabla; sumas, restas, y algo de
sentido común.
• Es buena idea ir construyendo la tabla y
comparar los resultados.

29. Tabla de simulación
Cliente Tiempo
desde la
última
llegada
(aleatorio)
Tiempo
de
llegada
Tiempo
de
servicio
(aleatorio)
Tiempo
de inicio
del
servicio
Tiempo
de
espera
en la
fila
Tiempo de
finalización
del
servicio
Tiempo que
el cliente
permanece
en el
sistema
Tiempo
ocioso
del
servidor
1 - 0 4 0 0 4 4 0
2 8 8 1 8 0 9 1 4
3 6 4
4
5
6
7
8
9
¿Cómo se
obtiene este
número nueve?

30. Tabla de simulación
Cliente Tiempo
desde la
última
llegada
(aleatorio)
Tiempo
de
llegada
Tiempo
de
servicio
(aleatorio)
Tiempo
de inicio
del
servicio
Tiempo
de
espera
en la fila
Tiempo de
finalización
del
servicio
Tiempo que
el cliente
permanece
en el sistema
Tiempo
ocioso
del
servidor
1 - 0 4 0 0 4 4 0
2 8 8 1 8 0 9 1 4
3 6 14 4 14 0 18 4 5
4 1 15 3 18 3 21 6 0
5 8 23 2 23 0 25 2 2
6 3 4
7
8
9

31. Tabla de simulación
Cliente Tiempo
desde la
última
llegada
(aleatorio)
Tiempo
de
llegada
Tiempo
de
servicio
(aleatorio)
Tiempo
de inicio
del
servicio
Tiempo
de
espera
en la fila
Tiempo de
finalización
del
servicio
Tiempo que
el cliente
permanece
en el
sistema
Tiempo
ocioso
del
servidor
1 - 0 4 0 0 4 4 0
2 8 8 1 8 0 9 1 4
3 6 14 4 14 0 18 4 5
4 1 15 3 18 3 21 6 0
5 8 23 2 23 0 25 2 2
6 3 26 4 26 0 30 4 1
7 8 5
8 7 4
9 2 5

32. Tabla de simulación
Cliente Tiempo
desde la
última
llegada
(aleatorio)
Tiempo
de
llegada
Tiempo
de
servicio
(aleatorio)
Tiempo
de inicio
del
servicio
Tiempo
de
espera
en la fila
Tiempo de
finalización
del
servicio
Tiempo que
el cliente
permanece
en el
sistema
Tiempo
ocioso
del
servidor
1 - 0 4 0 0 4 4 0
2 8 8 1 8 0 9 1 4
3 6 14 4 14 0 18 4 5
4 1 15 3 18 3 21 6 0
5 8 23 2 23 0 25 2 2
6 3 26 4 26 0 30 4 1
7 8 34 5 34 0 39 5 4
8 7 41 4 41 0 45 4 2
9 2 43 5 45 2 50 7 0
10 3 3

33. Tabla de simulación
Cliente Tiempo
desde la
última
llegada
(aleatorio)
Tiempo
de
llegada
Tiempo
de
servicio
(aleatorio)
Tiempo
de inicio
del
servicio
Tiempo
de
espera
en la fila
Tiempo de
finalización
del
servicio
Tiempo que
el cliente
permanece
en el
sistema
Tiempo
ocioso
del
servidor
1 - 0 4 0 0 4 4 0
2 8 8 1 8 0 9 1 4
3 6 14 4 14 0 18 4 5
4 1 15 3 18 3 21 6 0
5 8 23 2 23 0 25 2 2
6 3 26 4 26 0 30 4 1
7 8 34 5 34 0 39 5 4
8 7 41 4 41 0 45 4 2
9 2 43 5 45 2 50 7 0
10 3 46 3 50 4 53 7 0

34. Tabla de simulación
Cliente Tiempo
desde la
última
llegada
(aleatorio)
Tiempo
de
llegada
Tiempo
de
servicio
(aleatorio)
Tiempo
de inicio
del
servicio
Tiempo
de
espera
en la fila
Tiempo de
finalización
del
servicio
Tiempo que
le cliente
permanece
en el
sistema
Tiempo
ocioso
del
servidor
1 - 0 4 0 0 4 4 0
2 8 8 1 8 0 9 1 4
3 6 14 4 14 0 18 4 5
4 1 15 3 18 3 21 6 0
5 8 23 2 23 0 25 2 2
6 3 26 4 26 0 30 4 1
7 8 34 5 34 0 39 5 4
8 7 41 4 41 0 45 4 2
9 2 43 5 45 2 50 7 0
10 3 46 3 50 4 53 7 0
11 1 3
12 1 5
13 5 4

35. Tabla de simulación
Cliente Tiempo
desde la
última
llegada
(aleatorio)
Tiempo
de
llegada
Tiempo
de
servicio
(aleatorio)
Tiempo
de inicio
del
servicio
Tiempo
de
espera
en la fila
Tiempo de
finalización
del
servicio
Tiempo que
el cliente
permanece
en el
sistema
Tiempo
ocioso
del
servidor
1 - 0 4 0 0 4 4 0
2 8 8 1 8 0 9 1 4
3 6 14 4 14 0 18 4 5
4 1 15 3 18 3 21 6 0
5 8 23 2 23 0 25 2 2
6 3 26 4 26 0 30 4 1
7 8 34 5 34 0 39 5 4
8 7 41 4 41 0 45 4 2
9 2 43 5 45 2 50 7 0
10 3 46 3 50 4 53 7 0
11 1 47 3 53 6 56 9 0
12 1 48 5 56 8 61 13 0
13 5 53 4 61 8 65 12 0

36. Tabla de simulación
Cliente Tiempo
desde la
última
llegada
(aleatorio)
Tiempo de
llegada
Tiempo de
servicio
(aleatorio)
Tiempo de
inicio del
servicio
Tiempo de
espera en
la fila
Tiempo de
finalización
del servicio
Tiempo que el
cliente
permanece en
el sistema
Tiempo
ocioso del
servidor
1 - 0 4 0 0 4 4 0
2 8 8 1 8 0 9 1 4
3 6 14 4 14 0 18 4 5
4 1 15 3 18 3 21 6 0
5 8 23 2 23 0 25 2 2
6 3 26 4 26 0 30 4 1
7 8 34 5 34 0 39 5 4
8 7 41 4 41 0 45 4 2
9 2 43 5 45 2 50 7 0
10 3 46 3 50 4 53 7 0
11 1 47 3 53 6 56 9 0
12 1 48 5 56 8 61 13 0
13 5 53 4 61 8 65 12 0
14 6 1
15 3 5
16 8 4
17 1 3

37. Tabla de simulación
Cliente Tiempo
desde la
última
llegada
(aleatorio)
Tiempo de
llegada
Tiempo de
servicio
(aleatorio)
Tiempo de
inicio del
servicio
Tiempo de
espera en la
fila
Tiempo de
finalización
del servicio
Tiempo que
el cliente
permanece
en el
sistema
Tiempo
ocioso del
servidor
1 - 0 4 0 0 4 4 0
2 8 8 1 8 0 9 1 4
3 6 14 4 14 0 18 4 5
4 1 15 3 18 3 21 6 0
5 8 23 2 23 0 25 2 2
6 3 26 4 26 0 30 4 1
7 8 34 5 34 0 39 5 4
8 7 41 4 41 0 45 4 2
9 2 43 5 45 2 50 7 0
10 3 46 3 50 4 53 7 0
11 1 47 3 53 6 56 9 0
12 1 48 5 56 8 61 13 0
13 5 53 4 61 8 65 12 0
14 6 59 1 65 6 66 7 0
15 3 62 5 66 4 71 9 0
16 8 70 4 71 1 75 5 0
17 1 71 3 75 4 78 7 0

38. Tabla de simulación
Cliente Tiempo
desde la
última
llegada
(aleatorio)
Tiempo de
llegada
Tiempo de
servicio
(aleatorio)
Tiempo
de inicio
del
servicio
Tiempo de
espera en la
fila
Tiempo de
finalización del
servicio
Tiempo que el
cliente
permanece en
el sistema
Tiempo
ocioso del
servidor
1 - 0 4 0 0 4 4 0
2 8 8 1 8 0 9 1 4
3 6 14 4 14 0 18 4 5
4 1 15 3 18 3 21 6 0
5 8 23 2 23 0 25 2 2
6 3 26 4 26 0 30 4 1
7 8 34 5 34 0 39 5 4
8 7 41 4 41 0 45 4 2
9 2 43 5 45 2 50 7 0
10 3 46 3 50 4 53 7 0
11 1 47 3 53 6 56 9 0
12 1 48 5 56 8 61 13 0
13 5 53 4 61 8 65 12 0
14 6 59 1 65 6 66 7 0
15 3 62 5 66 4 71 9 0
16 8 70 4 71 1 75 5 0
17 1 71 3 75 4 78 7 0
18 2 3
19 4 2

39. Tabla de simulación
Cliente Tiempo
desde la
última
llegada
(aleatorio)
Tiempo de
llegada
Tiempo de
servicio
(aleatorio)
Tiempo de
inicio del
servicio
Tiempo
de
espera
en la fila
Tiempo de
finalización
del servicio
Tiempo que el
cliente
permanece en
el sistema
Tiempo ocioso
del servidor
1 - 0 4 0 0 4 4 0
2 8 8 1 8 0 9 1 4
3 6 14 4 14 0 18 4 5
4 1 15 3 18 3 21 6 0
5 8 23 2 23 0 25 2 2
6 3 26 4 26 0 30 4 1
7 8 34 5 34 0 39 5 4
8 7 41 4 41 0 45 4 2
9 2 43 5 45 2 50 7 0
10 3 46 3 50 4 53 7 0
11 1 47 3 53 6 56 9 0
12 1 48 5 56 8 61 13 0
13 5 53 4 61 8 65 12 0
14 6 59 1 65 6 66 7 0
15 3 62 5 66 4 71 9 0
16 8 70 4 71 1 75 5 0
17 1 71 3 75 4 78 7 0
18 2 73 3 78 5 81 8 0
19 4 77 2 81 4 83 6 0

40. Tabla de simulación
Cliente Tiempo desde
la última
llegada
(aleatorio)
Tiempo de
llegada
Tiempo de
servicio
(aleatorio)
Tiempo de
inicio del
servicio
Tiempo de
espera en la
fila
Tiempo de
finalización
del servicio
Tiempo que
el cliente
permanece
en el
sistema
Tiempo
ocioso del
servidor
1 - 0 4 0 0 4 4 0
2 8 8 1 8 0 9 1 4
3 6 14 4 14 0 18 4 5
4 1 15 3 18 3 21 6 0
5 8 23 2 23 0 25 2 2
6 3 26 4 26 0 30 4 1
7 8 34 5 34 0 39 5 4
8 7 41 4 41 0 45 4 2
9 2 43 5 45 2 50 7 0
10 3 46 3 50 4 53 7 0
11 1 47 3 53 6 56 9 0
12 1 48 5 56 8 61 13 0
13 5 53 4 61 8 65 12 0
14 6 59 1 65 6 66 7 0
15 3 62 5 66 4 71 9 0
16 8 70 4 71 1 75 5 0
17 1 71 3 75 4 78 7 0
18 2 73 3 78 5 81 8 0
19 4 77 2 81 4 83 6 0
20 5 82 3 83 1 86 4 0

41. Tabla de simulación
Cliente Tiempo
desde la
última
llegada
(aleatorio)
Tiempo de
llegada
Tiempo de
servicio
(aleatorio)
Tiempo de
inicio del
servicio
Tiempo de
espera en la
fila
Tiempo de
finalización
del servicio
Tiempo que
el cliente
permanece
en el
sistema
Tiempo
ocioso del
servidor
1 - 0 4 0 0 4 4 0
2 8 8 1 8 0 9 1 4
3 6 14 4 14 0 18 4 5
4 1 15 3 18 3 21 6 0
5 8 23 2 23 0 25 2 2
6 3 26 4 26 0 30 4 1
7 8 34 5 34 0 39 5 4
8 7 41 4 41 0 45 4 2
9 2 43 5 45 2 50 7 0
10 3 46 3 50 4 53 7 0
11 1 47 3 53 6 56 9 0
12 1 48 5 56 8 61 13 0
13 5 53 4 61 8 65 12 0
14 6 59 1 65 6 66 7 0
15 3 62 5 66 4 71 9 0
16 8 70 4 71 1 75 5 0
17 1 71 3 75 4 78 7 0
18 2 73 3 78 5 81 8 0
19 4 77 2 81 4 83 6 0
20 5 82 3 83 1 86 4 0
82 68 56 124 18

42. Análisis de resultados
• Tiempo promedio de espera en la fila.
• Probabilidad de que un cliente tenga que
esperar en la fila
𝑻𝒊𝒆𝒎𝒑𝒐 𝒕𝒐𝒕𝒂𝒍 𝒒𝒖𝒆 𝒍𝒐𝒔 𝒄𝒍𝒊𝒆𝒏𝒕𝒆𝒔 𝒆𝒔𝒑𝒆𝒓𝒂𝒏 𝒆𝒏 𝒍𝒂 𝒇𝒊𝒍𝒂
𝑵ú𝒎𝒆𝒓𝒐 𝒕𝒐𝒕𝒂𝒍 𝒅𝒆 𝒄𝒍𝒊𝒆𝒏𝒕𝒆𝒔
=
𝟓𝟔
𝟐𝟎
= 𝟐. 𝟖 (𝒎𝒊𝒏)
𝑵ú𝒎𝒆𝒓𝒐 𝒅𝒆 𝒄𝒍𝒊𝒆𝒏𝒕𝒆𝒔 𝒒𝒖𝒆 𝒆𝒔𝒑𝒆𝒓𝒂𝒓𝒐𝒏
𝑵ú𝒎𝒆𝒓𝒐 𝒕𝒐𝒕𝒂𝒍 𝒅𝒆 𝒄𝒍𝒊𝒆𝒏𝒕𝒆𝒔
=
𝟏𝟑
𝟐𝟎
= 𝟎. 𝟔𝟓

43. Análisis de resultados
• Probabilidad de servidor ocioso o fracción
de tiempo que permanece ocioso el servidor
• Probabilidad de que el servidor este
ocupado
1 – 0.21 = 0.79
𝑻𝒊𝒆𝒎𝒑𝒐 𝒕𝒐𝒕𝒂𝒍 𝒅𝒆𝒍 𝒔𝒆𝒓𝒗𝒊𝒅𝒐𝒓 𝒐𝒄𝒊𝒐𝒔𝒐
𝑻𝒊𝒆𝒎𝒑𝒐 𝒕𝒐𝒕𝒂𝒍 𝒅𝒆 𝒍𝒂 𝒔𝒊𝒎𝒖𝒍𝒂𝒄𝒊ó𝒏
=
𝟏𝟖
𝟖𝟔
= 𝟎. 𝟐𝟏

44. Análisis de resultados
• Tiempo promedio de servicio
• Comparar el resultado con el valor esperado a
partir de la tabla de distribución de
probabilidades de tiempo de atención
(Esperanza matemática)
E = 1(0.10) + 2(0.20) + 3(0.30) + 4(0.25) + 5(0.10) + 6(0.05) = 3.2
» Relación con la ley de los grandes números
𝑻𝒊𝒆𝒎𝒑𝒐 𝒕𝒐𝒕𝒂𝒍 𝒅𝒆 𝒔𝒆𝒓𝒗𝒊𝒄𝒊𝒐
𝑵ú𝒎𝒆𝒓𝒐 𝒕𝒐𝒕𝒂𝒍 𝒅𝒆 𝒄𝒍𝒊𝒆𝒏𝒕𝒆𝒔
=
𝟔𝟖
𝟐𝟎
= 𝟑. 𝟒 (𝒎𝒊𝒏)

45. Análisis de resultados
• Tiempo promedio entre llegadas.
• Comparar el resultado con el valor
esperado a partir de la tabla de distribución
de probabilidades de tiempo entre llegadas
(Esperanza matemática)
E = 1(0.125) + 2(0.125) … + 8(0.125) = 4.5
» Relación con la ley de los grandes números
𝑺𝒖𝒎𝒂 𝒅𝒆 𝒕𝒊𝒆𝒎𝒑𝒐𝒔 𝒆𝒏𝒕𝒓𝒆 𝒍𝒍𝒆𝒈𝒂𝒅𝒂𝒔
𝑵ú𝒎𝒆𝒓𝒐 𝒅𝒆 𝒍𝒍𝒆𝒈𝒂𝒅𝒂𝒔 − 𝟏
=
𝟖𝟐
𝟏𝟗
= 𝟒. 𝟑 (𝒎𝒊𝒏)

46. Análisis de resultados
• El tiempo promedio de espera se calculó
tomando en cuenta a clientes que, en
realidad, no esperaron, por ello, es
importante determinar el:
• Tiempo promedio de espera de los clientes
que realmente esperaron
𝑻𝒊𝒆𝒎𝒑𝒐 𝒕𝒐𝒕𝒂𝒍 𝒒𝒖𝒆 𝒍𝒐𝒔 𝒄𝒍𝒊𝒆𝒏𝒕𝒆𝒔 𝒆𝒔𝒑𝒆𝒓𝒂𝒓𝒐𝒏 𝒆𝒏 𝒍𝒂 𝒇𝒊𝒍𝒂
𝑻𝒐𝒕𝒂𝒍 𝒅𝒆 𝒄𝒍𝒊𝒆𝒏𝒕𝒆𝒔 𝒒𝒖𝒆 𝒓𝒆𝒂𝒍𝒎𝒆𝒏𝒕𝒆 𝒆𝒔𝒑𝒆𝒓𝒂𝒓𝒐𝒏
=
𝟓𝟔
𝟏𝟑
= 𝟒. 𝟑 (𝒎𝒊𝒏)

47. Análisis de resultados
• Tiempo promedio que un cliente
permanece en el sistema
• Comparar el resultado con la suma de
tiempos promedio en la fila más el
promedio de tiempo en el servidor
𝑻𝒊𝒆𝒎𝒑𝒐 𝒕𝒐𝒕𝒂𝒍 𝒒𝒖𝒆 𝒍𝒐𝒔 𝒄𝒍𝒊𝒆𝒏𝒕𝒆𝒔 𝒑𝒆𝒓𝒎𝒂𝒏𝒆𝒄𝒆𝒏 𝒆𝒏 𝒆𝒍 𝒔𝒊𝒔𝒕𝒆𝒎𝒂
𝑵ú𝒎𝒆𝒓𝒐 𝒕𝒐𝒕𝒂𝒍 𝒅𝒆 𝒄𝒍𝒊𝒆𝒏𝒕𝒆𝒔
=
𝟏𝟐𝟒
𝟐𝟎
= 𝟔. 𝟐 (𝒎𝒊𝒏)

48. Gracias
Gerardo Edgar Mata Ortiz
Twitter: @licemata
licmata@hotmail.com
https://sites.google.com/site/mataspc/
http://www.slideshare.net/licmata/
http://licmata-math.blogspot.com
http://licmata-ebc.blogspot.mx/
http://proc-industriales.blogspot.mx
http://www.facebook.com/licemata