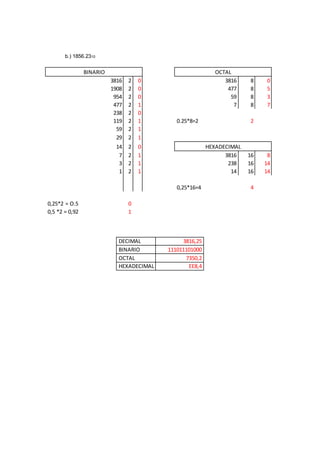
1. Se piden conversiones entre diferentes bases numéricas como binario, octal y hexadecimal. 2. Se solicitan operaciones como suma, resta, multiplicación y división utilizando complemento a dos y BCD. 3. Se plantean cálculos con números enteros y racionales aplicando conceptos como mínimo común múltiplo, módulo, exponenciación, funciones y aproximaciones.

1. TALLER DE MATEMATICAS DISCRETAS
TERCER CORTE
1. Convierta a binario, octal y hexadecimal los siguientes números en decimal:
a.) 854310
BINARIO OCTAL
8543 2 1 8543 8 7
4271 2 1 1067 8 3
2135 2 1 133 8 5
1067 2 1 16 8 0
533 2 1 2 8 2
266 2 0
133 2 1
66 2 0 HEXADECIMAL
33 2 1 8543 16 F
16 2 0 533 16 5
8 2 0 33 16 1
4 2 0 2 16 2
2 2 0
1 2 1
DECIMAL 8543
BINARIO 10000101011111
OCTAL 73502
HEXADECIMAL F512

2. b.) 1856.2310
BINARIO OCTAL
3816 2 0 3816 8 0
1908 2 0 477 8 5
954 2 0 59 8 3
477 2 1 7 8 7
238 2 0
119 2 1 0.25*8=2 2
59 2 1
29 2 1
14 2 0 HEXADECIMAL
7 2 1 3816 16 8
3 2 1 238 16 14
1 2 1 14 16 14
0,25*16=4 4
0,25*2 = O.5 0
0,5 *2 = 0,92 1
DECIMAL 3816,25
BINARIO 111011101000
OCTAL 7350,2
HEXADECIMAL EE8,4

3. c.) 3816.2510
BINARIO OCTAL
1856 2 0 1856 8 0
928 2 0 232 8 0
464 2 0 29 8 5
232 2 0 3 8 3
116 2 0
58 2 0 0.23*8=1,84 1
29 2 1 0.84*8=6,72 6
14 2 0 0.72*8=5,76 5
7 2 1 0.76*8=6,08 6
3 2 1 0.08*8=0,64 0
1 2 1
HEXADECIMAL
0,23*2=0,46 0 1856 16 0
0,46*2=0,92 0 116 16 4
0,92*2=1,84 1 7 16 7
0,84*2=1,68 1
0,68*2=1,36 1 0.23*16=3,68 3
0,36*2=0,72 0 0.68*16=10,88 A
0,72*2=1,44 1 0.88*16=14,08 E
0.08*16=1,28 1
0.28*16=4,48 4
0,48*16=7,68 7
DECIMAL 1856,23
BINARIO 11101000000,0011000
OCTAL 3500,16560
HEXADECIMAL 740,3AE147

4. 2. Convierta a decimal los siguientes números en su base indicada:
a.)72568 b.) 1E5C.2E16 c.) 1111000.1112
3. Calcule la adición y la sustracción por complemento la base, de los siguientes pares de
números:
1. (72568, 62868) b.) (1FE5C16, AFF5C16) c.) (11111000112, 11110000102)

5. 4. Sumar en BCD los siguientes números en decimal: a. 82 y 75, b. 469 y 386.

6. 5. Sumar los siguientes números enteros con signo en su equivalente de byte: a. (+16) con
(+25), b. (-26) con (+35), c. (-36) con (+20), d. (-56) con (-22).

7. 6. Calcule el mcd(245,105), mcd(440,225), mcd(1234,56); mediante la aplicación de los
algoritmos de:

8. 1. Descomposición en factores primos. b.) Diferencias. c.) Modulo de Euclides.

11. 7. Calcular: a.) 14852mod314. b.) 58mod200. c.) 1015mod61. d.) 14150mod532.
8. Utilice el método de exponenciación rápida (útil en técnicas de intercambio de clave y
firma digital), para calcular los valores de: a.) 2332mod51. b.) 100125mod201. C.)
125512mod2500

13. 9. Calcular: a.) Ø(17). b.) Ø(77). c.) Ø(200).
10. Elabore un breve resumen sobre el artículo denominado: “BASES MATEMÁTICAS
DESARROLLADAS EN EL AULA DE CLASE PARA LA SEGURIDAD DE LOS DATOS
EN REDES”, publicado en la revista universitaria ED N° 2 de 2014, página 59.
El artículo aborda la importancia de los fundamentos matemáticos dentro de los
cuales se basa la criptografía, la cual, es la ciencia que se ocupa de los procesos
que permiten la alteración de las representaciones lingüísticas de los mensajes,
utilizando diferentes técnicas de cifrado con el fin de adquirir un nivel de
confidencialidad entre estos. Con la necesidad que ha surgido por mantener segura
los diferentes tipos de información, se han adoptado modelos matemáticos que
permitan crear algoritmos con cierto nivel de complejidad y con números grandes de
difícil simplificación. Algunos datos históricos importantes es que el término de
criptografía no es nuevo y se ha usado por muchos siglos, se usó en un sistema de
sustitución basado en la posición de letras de tablero de ajedrez, en sistema llamado
Cesar, en un tratado de escritura secreta, en un complot hacia la reina por usar
criptoanálisis, en la 1 guerra mundial, en máquinas de cálculo conocida como
enigma para arrojar cálculos cifrados de mensajes, para la derrota del ingenio
alemán, investigaciones de Claude Shannon, en diseño lógico de un cifrado. Como
conclusión tenemos que la criptografía se ha venido desarrollando a través de los
tiempos haciendo el uso de la tecnología; su importancia ha tomado cada vez más
fuerza debido a que existe información de un nivel de confidencialidad muy alto por
lo cual es necesario hallar un método para protegerla de intrusos, a través de la
aritmética modular como base de codificación y decodificación de la información.

14. 11. Utilice la expresión de aproximación RSA (n + 15)mod28, para cifrar las siguientes
palabras: a.) ENCRIPTAR EL MUNDO. b.) LA CALLE ESTA ILUMINADA c.)BOLIVAR
EL LIBERTADOR. Aplique ahora la expresión (n-15)mod28 para descifrar estos
mensajes.
A 1
B 2
C 3
D 4
E 5
F 6
G 7
H 8
I 9
J 10
K 11
L 12
M 13
N 14
O 15
P 16
Q 17
R 18
S 19
T 20
U 21
V 22
W 23
X 24
Y 25
Z 26
– 27

15. A) ENCRIPTAR EL MUNDO
E (5 + 15) mod28 = 20 T
N (14 + 15) mod28 = 1 A
C (3 + 15) mod28 = 18 R
R (18 + 15) mod28 = 5 E
I (9 + 15) mod28 = 24 X
P (16 + 15) mod28 = 3 C
T (20 + 15) mod28 = 7 G
A (1 + 15) mod28 = 16 P
R (18 + 15) mod28 = 5 E
– (27 + 15) mod28 = 14 N
E (5 + 15) mod28 = 20 T
L (12 + 15) mod28 = 27 –
– (27 + 15) mod28 = 14 N
M (13 + 15) mod28 = 0 O
U (21 + 15) mod28 = 8 H
N (14 + 15) mod28 = 1 A
D (4 + 15) mod28 = 19 S
O (15 + 15) mod28 = 2 B

16. B) LA CALLE ESTA ILUMINADA
L (12 + 15) mod28 = 27 –
A (1 + 15) mod28 = 16 P
– (27 + 15) mod28 = 14 N
C (3 + 15) mod28 = 18 R
A (1 + 15) mod28 = 16 P
L (12 + 15) mod28 = 27 –
L (12 + 15) mod28 = 27 –
E (5 + 15) mod28 = 20 T
– (27 + 15) mod28 = 14 N
E (5 + 15) mod28 = 20 T
S (19 + 15) mod28 = 6 F
T (20 + 15) mod28 = 7 G
A (1 + 15) mod28 = 16 P
– (27 + 15) mod28 = 14 N
I (9 + 15) mod28 = 24 X
L (12 + 15) mod28 = 27 –
U (21 + 15) mod28 = 8 H
M (13 + 15) mod28 = 0 O
I (9 + 15) mod28 = 24 X
N (14 + 15) mod28 = 1 A
A (1 + 15) mod28 = 16 P
D (4 + 15) mod28 = 19 S
A (1 + 15) mod28 = 16 P

17. C) BOLIVAR EL LIBERTADOR
B (2 + 15) mod28 =17 Q
O (15 + 15) mod28 = 2 B
L (12 + 15) mod28 = 27 –
I (9 + 15) mod28 = 24 X
V (22 + 15) mod28 = 9 I
A (1 + 15) mod28 = 16 P
R (18 + 15) mod28 = 5 E
– (27 + 15) mod28 = 14 N
E (5 + 15) mod28 = 10 T
L (12 + 15) mod28 = 27 –
– (27 + 15) mod28 = 14 N
L (12 + 15) mod28 = 27 –
I (9 + 15) mod28 = 24 X
B (2 + 15) mod28 = 17 Q
E (5 + 15) mod28 = 20 T
R (18 + 15) mod28 = 5 E
T (20 + 15) mod28 = 7 G
A (1 + 15) mod28 = 16 P
D (4 + 15) mod28 = 19 S
O (15 + 15) mod28 = 2 B
R (18 + 15) mod28 = 5 E

18. 12. Sean p=17, q=23, n=31. Aplique el método RSA de encriptado para realizar los
siguientes cálculos: z, Ø, s; cifre 101, 200; descifre 300, 250.
Z= p*q
Z= 17*23
Z=391
∅=(P-1)(q-1)
∅=16*22
∅=352
𝑠 = 863
a).101
10131
mod 391= 186
101 cifradoes186
b).200
20031
mod 391=123
200 cifradoes123
c).300
300863
mod391=116
300 descifradoes116
d).250
250863
mod391=10
250 descifradoes10
13. Encontrar una fórmula que sea recurrente, de tal manera que sirva para digitalizar las
siguientes funciones: a.) Sen2X, b.) CosX, c.) e3x con la aproximación de cinco derivadas
e implemente la codificación respectiva en Matlab.
a). Sen2X
Sen2XF(X)=Sen(2X) f(0)=0
f’(X)=2Cos(X)f(0)=2
f’’(X)=-4Sen(2X) f(0)=0
f’’’(X)=-8Cos(2X) f(0)=-8
f4
(X)=16Sen(2X) f(0)=0
f5
(X)=32Cos(2X) f(0)=32
Sen(2x)=∑ (−1) 𝑛+122𝑛−1 𝑋2𝑛−1∞
𝑛=1
2n-1

19. b). CosX
f(X)=Cos(X) f(0)=1
f’(X)=-Sen(X)f(0)=0
f’’(X)=-Cos(X) f(0)=-1
f’’’(X)=Sen(X) f(0)=0
f4
(X)=Cos(X) f(0)=1
f5
(X)=-Sen(X) f(0)=0
Cos(x)=1+∑ (−1) 𝑛 𝑋2𝑛∞
𝑛=1
2n!
c). e3x
f (X)= e3x
f(0)=1
f’ (X)= 3e3x
f(0)=3
f’’(X)= 32
e3x
f(0)=9
f’’’(X)= 33
e3x
f(0)=27
f4
(X)= 34
e3x
f(0)=81
f5
(X)= 35
e3x
f(0)=243
e3x
=1+∑ (3) 𝑛 𝑋 𝑛∞
𝑛=1
n!

20. 14. Calcule lascombinacionesypermutacionesindicadas: a.) 7C3 y7P3. b.) 10C2 y 10P2
c.) 16C4 y 16P4.
a).
(7
3
)=
7!
3!(7−3)

7!
3!(4)
(7
3
)=
7∗6∗5∗4
3∗2∗1∗4
 35
(7
3
)=
7!
(7−3)

7!
4!
(7
3
)=
7∗6∗5∗4
4
 210
b).
(10
2
)=
10!
2!(10−2)

10!
2!(8)
(10
2
)=
10∗9∗8
2∗1∗8
 45
(10
2
)=
10!
(10−2)

10!
8!
(10
2
)=
10∗9∗8
8
 210
c).
(16
4
)=
16!
4!(16−4)

16!
4!(12)
(16
4
)=
16∗15∗14∗13∗12
4∗3∗2∗1∗12
 1820
(16
4
)=
16!
(16−4)

16!
12!
(16
4
)=
16∗15∗14∗13∗12
12
 43680

21. 15. Utilice la combinatoria para hacer la expansión de los siguientes binomios: a.) (x – 3)6;
b.) (x + 5)8; c.) (2 + y) 10.
a).
b).
(
8
0
) =
8!
0!8!
= 1𝑥8 (5)0 = 1
(
8
1
) =
8!
1!7!
=
8 ∗ 7
1 ∗ 7
= 8𝑥7 (5)1 = 5
(
8
2
) =
8!
2!6!
=
8 ∗ 7 ∗ 6
2! 6!
= 28𝑥6 (5)2 = 25
(8
3
) =
8!
3!5!
=
8∗7∗6∗5
3!5!
= 56𝑥5 (5)3 =125
(
8
4
) =
8!
4!4!
=
8 ∗ 7 ∗ 6 ∗ 5 ∗ 4
4! 4!
= 70𝑥4 (5)4 = 625
(
8
5
) =
8!
5!3!
=
8 ∗ 7 ∗ 6 ∗ 5
5! 3!
= 56𝑥3 (5)5 = 3125
(
8
6
) =
8!
6!2!
=
8 ∗ 7 ∗ 6
6! 2!
= 28𝑥2 (5)6 = 15625
(
8
7
) =
8!
7!1!
=
8 ∗ 7
7! 1!
= 8𝑥1 (5)7 = 78125
(
8
8
) =
8!
8!0!
= 1𝑥0 (5)8 = 390625
(x+5)8=x8+40x7+700x6+7000x5+43750x4+175000x3+437500x2+625000x1+390625

22. 16. Una clase se compone de 12 niños y 10 niñas. Hallar el número de posibilidades que
tiene un profesor de elegir un comité de: a.) de 6. b.) 4 niños y 3 niñas. c.) 4 niños o 4
niñas. d.) Al menos una niña.
a).
(
22
6
) =
22!
6! (22 − 6)
=
22 ∗ 21 ∗ 20 ∗ 19 ∗ 18 ∗ 17 ∗ 16
6! (16)
=
22 ∗ 21 ∗ 20 ∗ 19 ∗ 18 ∗ 17
6!
= 74613
b).
(
12
4
) ∗ (
10
3
) =
12!
4! (12 − 4)
∗
10!
3!(10 − 3)
=
12 ∗ 11 ∗ 10 ∗ 9 ∗ 8
4!(8)
∗
10 ∗ 9 ∗ 8 ∗ 7
3!(7)
= 59400
c).
(
12
4
) + (
10
3
) =
12!
4! (12 − 4)
+
10!
4! (10 − 4)
=
12 ∗ 11 ∗ 10 ∗ 9 ∗ 8
4! (8)
+
10 ∗ 9 ∗ 8 ∗ 7 ∗ 6
4! (6)
= 705
d).
(
10
1
) =
10!
1! (10 − 1)
=
10 ∗ 9
1! (9)
= 10
17. Cuántas palabras o cifras se pueden expresar con los elementos de los siguientes
conjuntos: a.) {C,A,M,I,S.A} b.) {2,4,6,8} c.) {m,u,r,c,i,e,l,a,g,o}
a).C A M I S A
6!
0!
=
6 ∗ 5 ∗ 4 ∗ 3 ∗ 2 ∗ 1
1
= 720 𝑃𝑎𝑙𝑎𝑏𝑟𝑎𝑠
b).2,4,6,8
4! = 4*3*2*1=24 Cifras
c). M U R C I E L A G O
10!
0!
=
10 ∗ 9 ∗ 8 ∗ 7 ∗ 6 ∗ 5 ∗ 4 ∗ 3 ∗ 2 ∗ 1
1
= 3628800 𝑃𝑎𝑙𝑎𝑏𝑟𝑎𝑠

23. 18. Se tira un par de dados. Sea X el menor de los dos números que salen. Determinar el
espacio muestral, el rango RX, la distribución de probabilidad y la esperanza de X.
●
●
●
●
●
●
● ●
● ●
● ●
●
● ●
● ●
● ●
● ●
● (1,1ꓲ 1) (1,2ꓲ 1) (1,3ꓲ 1) (1,4ꓲ 1) (1,5ꓲ 1) (1,6ꓲ 1)
●
●
(2,1ꓲ 1) (2,2ꓲ 2) (2,3ꓲ 2) (2,4ꓲ 2) (2,5ꓲ 2) (2,6ꓲ 2)
●
●
●
(3,1ꓲ 1) (3,2ꓲ 2) (3,3ꓲ 3) (3,4ꓲ 3) (3,5ꓲ 3) (3,6ꓲ 3)
● ●
● ●
(4,1ꓲ 1) (4,2ꓲ 2) (4,3ꓲ 3) (4,4ꓲ 4) (4,5ꓲ 4) (4,6ꓲ 4)
● ●
●
● ●
(5,1ꓲ 1) (5,2ꓲ 2) (5,3ꓲ 3) (5,4ꓲ 5) (5,5ꓲ 5) (5,6ꓲ 5)
● ●
● ●
● ●
(6,1ꓲ 1) (6,2ꓲ 2) (6,3ꓲ 3) (6,4ꓲ 4) (6,5ꓲ 5) (6,6ꓲ 6)
X 2 3 4 5 6 7 8 9 10 11 12
F(X) 1/36 2/36 3/36 4/36 5/36 6/36 5/36 4/36 3/36 2/36 1/36
E(X) 2/36 6/36 12/36 20/36 30/36 42/36 40/36 36/36 30/36 22/36 12/36
Var(X)=
4
36
+
18
36
+
48
36
+
100
36
+
180
36
+
294
36
+
320
36
+
324
36
+
300
36
+
242
36
+
144
36
− (6)2
Var(X)=
1974
36
−
36
1
=
113
6
= 18.83

24. 19. Un jugador tira tres monedas. Gana $500 si salen tres caras, $300 si salen dos caras y
$100 si sale una. Por otra parte, pierde $1000 si salen tres sellos. Hallar el valor del juego
para el jugador.
S = {CCC, CCS, CSS, SSS, SSC, SCC, CSC, SCS}
Gana $500 con CCC
Gana $300 con CCS, SCC, CSC
Gana $100 con CSS, SSC, SCS
CCC = $500 $500
CCS = $300
SCC = $300 $900 $700
CSC = $300
CSS = $100
SSC = $100 $300
SCS = $100
SSS = $1000 $1000

25. 20. Calcular la media, la varianza y la desviación típica de la siguiente distribución: Elabore
un gráfico de barras.
X 5 2 3 4 6 7 9 12 11 9
F(x) 0.1 0.2 0.05 0.05 0.2 0.1 0.05 0.05 0.05 0.15
21. Considere la distribución conjunta de X e Y que se muestra en la siguiente tabla. Con los
datos consignados allí, determine: E(X), E(Y), cov(X,Y), σX, σY y ρ(X,Y).
XY -2 -1 4 5 Suma
1 0.1 0.2 0 0.3 0.6
2 0.2 0.1 0.1 0 0.4
Suma 0.3 0.3 0.1 0.3 1.0
Cov XY = EE, (Y) (XY) - (UX, MY)
Cov XY=602-0.2+0+1.5+0.8+0.5-(1.4) (1.0)
Cov XY=1.4-0.84=0.56
Var(X)=0.24
B(X)- V 0.24 = 0.4898
Var (y)=9.6
B(y)=V 9.6=3.0983
P(xy)=(0.56) / (0.498) (3.0983) = 0.3629 < 1