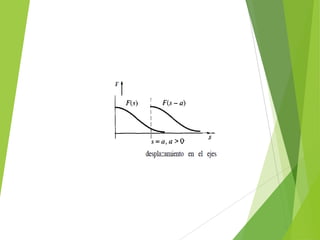
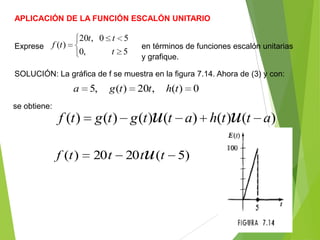
El documento presenta información sobre la transformada de Laplace. Introduce el primer teorema de traslación, el cual establece que la transformada de Laplace de una función desplazada en el eje de tiempo es igual a la transformada de la función original evaluada en una variable desplazada. También presenta demostraciones de este teorema y ejemplos de su aplicación.

1. Escuela
Politécnica
Nacional
Transformada de Laplace

2. Integrantes
 Velasco Kevin
 Tacan Deysi
 Chirau Diana
 Cerón Laura

3. Primer teorema de traslación
No es adecuado utilizar la definición cada vez
que se quiera calcular una transformada, por
ejemplo, la integración por
partes involucrada al calcular
es bastante tediosa. Por esta razón vamos a
enunciar algunos teoremas que ahorran trabajo
en el cálculo de este tipo de transformadas.

4. Primer teorema de
traslación
)( ass

6. Demostración
Recurriendo a la definición de la transformada de Laplace
tenemos:
Recordando la forma como se calculan las integrales
impropias y las propiedades de los límites:

7. Agrupando las funciones exponenciales:
Si ahora hacemos el cambio de variable S=s-a lo
anterior queda:

8. Este segundo miembro coincide con la transformada
de laplace de la función f(t) en la variable S
siempre y cuando S > 0 , es decir siempre que
s-a > 0, es decir s > a. Resumiendo
Donde
Si encadenamos esta serie de igualdades

9. Ejemplo 1:
ℒ 𝑒5𝑡
𝑡3
= ℒ 𝑡3
)5(ss =
3!
𝑠4 4)5(
1.2.3
s
ss )5(ss = 4
)5(
6
s
Ejemplo 2:
ℒ 𝑒−2𝑡
cos 4𝑡 = ℒ cos 4𝑡 )2(ss
2a
2)2( ssas
ℒ cos 4𝑡 )2(ss =
𝑠
=
ℒ 𝑒−2𝑡
cos 4𝑡 = ℒ cos 4𝑡 )2(ss
2a
2)2( ssas
ℒ cos 4𝑡 )2(ss =
𝑠
𝑠2 + 16 )2(ss =
16)2(
2
2
s
s
os 4𝑡 = ℒ cos 4𝑡 )2(ss
2)2( ss
ℒ cos 4𝑡 )2(ss =
𝑠
𝑠2 + 16 )2(ss =
16)2(
2
2
s
s
ℒ 𝑒5𝑡
𝑡3
= ℒ 𝑡3
)5(ss =
3!
𝑠4 4)5(
1.2.3
s
ss )5(ss = 4
)5(
6
s

10. Forma inversa del primer teorema
de traslación
inversa del teorema es:
ℒ−1
{𝐹 𝑠 − 𝑎 = ℒ−1
)()( asssF = 𝑒 𝑎𝑡
𝑓 𝑡

11. Ejemplo:

13. CONCEPTO: En ingeniería se presentan con mucha frecuencia funciones que
están ya sea “desactivadas” o “activadas”. Por ejemplo, una fuerza externa que
actúa sobre un sistema mecánico o un voltaje aplicado a un circuito, se puede
desactivar después de cierto tiempo. Así, es inconviente definir una función
especial que es el número 0 (desactivada) hasta un cierto tiempo t = y luego el
número 1 (activada) después de ese tiempo. La función se llama función
escalón unitario o función de Heaviside.
DEFINICIÓN DE FUNCIÓN ESCALÓN UNITARIO
La función escalón unitario se define como:)( atu
at
at
atu
,1
0,0
)(
(2)

14. LA FUNCIÓN ESCALÓN UNITARIO EN FUNCIONES DEFINIDAS POR PARTES
La función escalón unitario se puede usar para escribir funciones definidas por
partes en una forma compacta o también cuando la función esta definida por
partes en forma general como los siguientes tipos:
)()()()()()(
),(
0),(
)( atthattgtgtf
atth
attg
tf uu (3)
)()()()(
,0
),(
0,0
)( btattgtf
bt•
btatg
at
tf uu (4)

15. APLICACIÓN DE LA FUNCIÓN ESCALÓN UNITARIO
Exprese en términos de funciones escalón unitarias
5,0
50,20
)(
t
tt
tf
y grafique.
SOLUCIÓN: La gráfica de f se muestra en la figura 7.14. Ahora de (3) y con:
0)(,20)(,5 thttga
se obtiene:
)()()()()()( atthattgtgtf uu
)5(2020)( ttttf u

16. SEGUNDO TEOREMA DE TRASLACION
Demostración

18. Forma alternativa del segundo teorema de
traslación

20. Forma inversa del segundo teorema de
traslación

21. Solución:

22. DERIVADA DE LA
TRANSFORMADA DE LAPLACE
)(
)(
)()(
)()(
0
0
0
ttfL
dtttfe
dttfe
ds
d
sF
ds
d
dttfesF
st
st
st

23. PARA LA SEGUNDA
DERIVADA
Por Inducción
)(
)(
)()(
)()(
0
0
0
ttfL
dtttfe
dttfe
ds
d
sF
ds
d
dttfesF
st
st
st

24. EJEMPLO