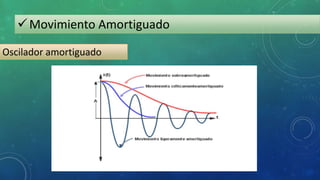
El documento describe tres tipos de movimiento: movimiento no amortiguado, movimiento amortiguado y movimiento forzado. El movimiento no amortiguado sigue la ley de Hooke y ecuaciones diferenciales simples. El movimiento amortiguado considera fuerzas de fricción que disipan la energía del sistema sobre el tiempo. El movimiento forzado analiza sistemas oscilatorios sujetos a fuerzas externas periódicas, resultando en soluciones transitorias y estacionarias.

1. • Movimiento no Amortiguado
• Movimiento Amortiguado
• Movimiento forzado

2. Movimiento NO Amortiguado
Oscilaciones

3.  Sistema resorte/masa, movimiento libre no amortiguado
Ley de Hooke

4.  Sistema resorte/masa, movimiento libre no amortiguado
Segunda Ley de Newton

5.  Sistema resorte/masa, movimiento libre no amortiguado
Ecuación Diferencial

6.  Sistema resorte/masa, movimiento libre no amortiguado
Ecuación Diferencial
Términos de uso frecuente:

7. Movimiento Amortiguado
Oscilador amortiguado
Todos los osciladores reales están sometidos a alguna fricción. Las fuerzas de fricción
son disipativas y el trabajo que realizan es transformado en calor que es disipado
fuera del sistema. Como consecuencia, el movimiento está amortiguado, salvo que
alguna fuerza externa lo mantenga. Cuando el amortiguamiento no supera este valor
crítico el sistema realiza un movimiento ligeramente amortiguado, semejante al
movimiento armónico simple, pero con una amplitud que disminuye
exponencialmente con el tiempo.

8. Movimiento Amortiguado
Oscilador amortiguado

9. Movimiento Amortiguado
Oscilador amortiguado
En todos los casos físicos existe alguna fuerza de rozamiento que generalmente se
considera proporcional a la velocidad quedando la ecuación diferencial de movimiento
Consideremos una masa m en una posición de equilibrio y sujeta a una fuerza de recuperación
proporcional al desplazamiento x del equilibrio y opuesta a él según la ecuación
F= -kx

10. Movimiento Amortiguado
Oscilador amortiguado
donde b es la constante de amortiguamiento. Dado que Fr se opone al
movimiento, signo opuesto a la velocidad del objeto, realiza un trabajo negativo y es la
causa de que la energía disminuya. Introducido este término en la 2º ley de Newton
obtenemos la ecuación diferencial de movimiento de un sistema amortiguado.

11. Movimiento Amortiguado
Oscilador sobre amortiguado
En este caso el sistema no es realmente un oscilador, ya que no oscila. La solución es
de la forma: En este caso el sistema no es realmente un oscilador, ya que no oscila. La
solución es de la forma:
donde los coeficientes de las exponenciales son menores que cero y reales :

12. Movimiento Amortiguado
Oscilador con Amortiguamiento Crítico
Este caso es el límite entre un sistema oscilante y uno no oscilante. Ocurre
cuando
La solución única es:

13. Movimiento Amortiguado
Oscilador con Amortiguamiento Débil
En este caso, tenemos un oscilador que oscila alrededor de la posición de equilibrio con amplitud decreciente.
Sucede cuando:
Al dividir la ecuación por la masa m, la ecuación diferencial del movimiento amortiguado

14. Movimiento Amortiguado
Oscilador con Amortiguamiento Débil
CASO III: ʎ ^2 – w^2< 0

15. Movimiento Forzado
Movimiento Forzado con Amortiguamiento
Ahora tomaremos en cuenta una fuerza externa, f(t), que actúa sobre una masa
oscilatoria en un resorte; por ejemplo, f(t) podría representar una fuerza de impulsión
que causara un movimiento oscilatorio vertical del soporte del resorte (Véase la figura).
La inclusión de y(t) en la formulación de la segunda ley de Newton da la ecuación
diferencial del movimiento forzado:
Al dividir esta ecuación por m se obtiene

16. Movimiento Forzado
Movimiento Forzado con Amortiguamiento
Para resolver esta ecuación no homogénea tenemos el
método de los coeficientes indeterminados o el de la
variación de parámetros.

17. Movimiento Forzado
Términos Transitorios y Estacionarios
Cuando f es una función periódica como:
Consiste en: X= Termino transitorio + Termino estacionario
La solución general de la ecuación

18. Movimiento Forzado
Términos Transitorios y Estacionarios
en el entendido que a la solución que encontremos debemos quedarnos con la parte real. La solución
puede adivinarse de la forma
Una solución particular.
Si la fuerza forzadora es periódica de la forma

19. Ahora damos paso a:
Ejercicios y Problemas