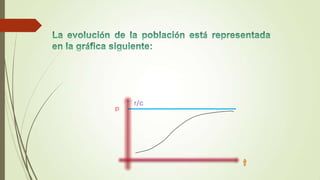
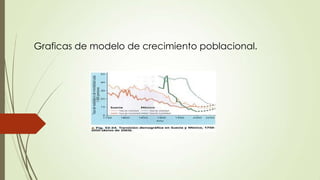
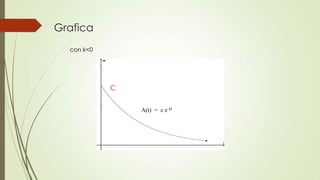
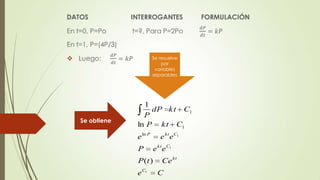
Este documento presenta información sobre modelos matemáticos de crecimiento poblacional y descomposición radiactiva. Incluye una reseña histórica de Robert Malthus y su modelo de crecimiento poblacional, así como ejemplos y ecuaciones para modelar el crecimiento de una población con respecto al tiempo. También cubre la descomposición radiactiva, incluyendo una breve historia y ecuaciones para modelar la descomposición de una sustancia radiactiva a lo largo del tiempo.

1. Ecuaciones Diferenciales
Modelos matemáticos

2. Escuela Politécnica Nacional
Integrantes:
Cerón Laura
Chirau Diana
Tacàn Deysi
Velasco Kevin

3. CRECIMIENTO POBLACIONAL

4. RESEÑA HISTÓRICA
 Robert Malthus fue una de las primeras personas que
estudio el crecimiento demográfico.
 El libro “ENSAYO SOBRE EL PRINCIPIO DE LA
POBLACIÓN” de Robert Malthus, fue muy celebre en 1798.
 Sus ideas tuvieron alguna influencia en la teoría de la
evolución de Darwin.

5. MARCO TEÓRICO
Lo que veremos a continuación será modelo de
ecuaciones diferenciales aplicadas al crecimiento
poblacional, en donde se puede constatar que la
población evoluciona conforme pasa el tiempo P(t).
Esta variación se da debido a que todos los seres vivos
cumplen con el ciclo biológico de nacer, crecer,
reproducir y morir. Esto se da en todas las poblaciones
como bacterias, hongos, animales, seres humanos, etc.
Pero lo que mas afecta a la variación de la población
son los nacimientos, y muertes.

6. Modelo de Malthus
Fue al parecer Euler quien desarrolló los primeros modelos
de población, pero comúnmente se atribuye a Malthus el
desarrollo y análisis del primer modelo de evolución de
P(t), según el cual:
Es decir, en cada instante la rapidez de cambio de la
población es proporcional al total de la población
presente. Por ejemplo, si P(t) >= 0 y P(t ) creciente, esto
implica que k > 0.

7. Resolvemos la ecuación diferencial
Integrando se tiene:

8. Aunque hemos visto que el modelo funciona
razonablemente bien para poblaciones grandes, hay que
hacer varias correcciones pues si P(t) empieza a crecer
demasiado habrá muchos otros factores como la falta de
espacio o de alimentos que frenará el crecimiento.

9. ab ǂ 0
dp
dt
p(r cp)
dp 1 p
log t C
p(r cp) r r cp
p
Ce rt como p(to) po asi que
r cp
p p (o) r t to
e
r cp r cp(o)

10. r/c
p

11. Graficas de modelo de crecimiento poblacional.

12. DESCOMPOSICIÓN RADIACTIVA

13. Reseña histórica
• Poco después de que se descubriera los
rayos X, en 1895, Antoine Henri Becquerel
(1852-1908) trató de demostrar la relación
entre los rayos X y la fosforescencia de las
sales de uranio.
• Envolvió una placa fotográfica en papel
negro, colocó una muestra de sal de uranio
sobre ella y la expuso a la luz solar.

14. • Al revelar la placa apareció que los rayos emitidos por la
sal habían penetrado a través del papel.
• Repitió el experimento en la oscuridad total y obtuvo los
mismos resultados
• Probando así que la sal de uranio emitía rayos que
afectaban la emulsión fotográfica, sin necesidad de ser
expuesta a la luz solar. De este modo fue que Becquerel
descubrió la radiactividad.

15. • Radiactividad es la emisión espontánea de partículas o
rayos por el núcleo de un átomo. A los elementos que
tienen esta propiedad se les llama radiactivos.
• Ernest Rutherford, en 1899, comenzó a investigar la
naturaleza de los rayos emitidos por el uranio. Encontró
dos tipos de rayos, a los que llamó rayos alfa y beta.
• A la altura de 1912 se conocían ya más de 30 isótopos
radiactivos y hoy se conocen mucho más.
• Paul Villard descubrió en 1900, los rayos gamma, un
tercer tipo de rayos que emiten los materiales
radiactivos y que es semejante a los rayos X.

17. dA  Donde k<0 representa un decrecimiento e
kA n la masa atómica
dt

18. Grafica
con k<0
C
A(t) = c e kt

19. Ejercicios de Aplicación
Crecimiento Poblacional

20. Ejemplo general
 Un cultivo de células dispuestas en un laboratorio tiene una
cantidad inicial Po, al transcurrir una hora, el analista observa
que la cantidad es 4/3 de la cantidad inicial; si se sabe que la
rapidez del crecimiento en la población es proporcional a la
cantidad de células presentes. Cuál será el tiempo necesario
para que la población se haya duplicado?

21. Se resuelve
por
variables
separables
1
dP kt C1
P
Se obtiene
ln P kt C1
e ln P e kt e C1
P e kt e C1
P (t ) Ce kt
e C1 C

22. Para conocer las variables se utiliza las condiciones valor inicial
ENTONCES :
Sabemos que en t=0, P=Po
P (t ) Ce kt
P (t ) Ce kt P0 Ce k ( 0 )
P0 C
En los datos del problema también se conoce que
en t=1, P=(4Po/3), de lo que obtenemos
4 4
P P0 P0 P0 e k (1)
3 3
4
ln k
3
k 0.2876

23. Con los datos calculados, se puede decir que la población
en cualquier instante esta determinada por la siguiente
ecuación:
0.2876t
P(t ) 0Pe
Con la ecuación encontrada, se puede responder a la
pregunta planteada en el ejercicio planteado.
t=?, para que P=Po 0.2876t
2 P0 P0 e
ln 2 0.2876t
ln 2
t 2.410
0.2876

24. Modelo de Malthus
 En un cultivo de bacterias, se estimó que inicialmente había 150
bacterias y 200 después de una hora (h). Suponiendo una rapidez
de crecimiento proporcional a la cantidad de bacterias presente,
determinar:
 La cantidad de bacterias después de t horas.
 El tiempo que debe transcurrir para que la población se
triplique.

25. Si P (t) es la cantidad de bacterias presentes después de t horas, entonces P
(0)= Po = 150 y P (1)= P1 = 200

26. Para que la población se triplique:

27. Modelo Logístico
dp
kp (I E)
dt
p' k p I E
kdt
e e kt
kt dp
e e kt ( k p) e kt ( I E)
dt
d (e kt p )
e kt ( I E )
dt
kt kt
(e p) e (I E)
kt
kt e
p e (I E) c
k
(I E)
p ce kt
k

28. P(t ) Poe kt
P´(t ) kPoekt
P´(0) kPo
P(0) (0.00022)(365.25) 0.0804 miles de millones por año

29. Ejercicios de Aplicación
Descomposición Radiactiva

30. Ejercicio
La conversión de una sustancia B sigue la ley de
descomposición. Si solo tres cuartas partes de la sustancia ha
sido convertida después de diez segundos. Encuéntrese
cuanto tardan en convertir 1/10 de la sustancia.
Solución:
X: es la cantidad de sustancia B
Según los datos se tiene
X Xo 3/4X0 X0/10
t 0 10 t

31. 
dx
kx
dt

32. OBSERVACIONES
 Los modelos matemáticos son uno de los tipos de modelos científicos que
emplea algún tipo de formulismo matemático para expresar relaciones,
proposiciones sustantivas de hechos, variables, parámetros, entidades y
relaciones entre variables y/o entidades u operaciones, para estudiar
comportamientos de sistemas complejos ante situaciones difíciles de
observar en la realidad.
 Una de las herramientas mas interesantes que actualmente disponemos
para analizar y predecir el comportamiento de un sistema biológico es la
construcción y posterior simulación de un modelo matemático. Son
muchas las razones que justifican la edad de oro que hoy en día vive la
modelización matemática, pero debemos de destacar, en primer lugar, el
mejor conocimiento de los procesos biológicos, y en segundo lugar, el
espectacular avance de los ordenadores y el software matemático.

33. CONCLUCIONES
 El uso de modelados matemáticos como herramientas que facilitan
el desarrollo de problemas resultan de gran utilidad, ya que de entre
todas sus aplicaciones en las ecuaciones diferenciales permiten
conocer aproximaciones de resultados que se podrían necesitar
para el planteamiento de cierto proyecto laboral educativo u
empresarial.
 A partir de una ecuación diferencial se puede calcular y modelar el
crecimiento o decrecimiento de una determinada población, y
predecir la variación de dicha población con respecto al tiempo.