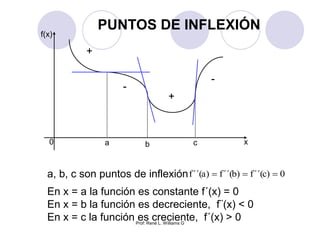
Este documento presenta conceptos fundamentales del cálculo diferencial como límites, continuidad funcional y derivada. Explica que un límite representa el valor al que se acerca una función al acercarse a un punto, y que la derivada de una función en un punto es igual a la pendiente de la tangente en ese punto. También incluye reglas para calcular derivadas y la relación entre continuidad y derivabilidad.









![Prof: René L. Williams G
CONTINUIDAD FUNCIONAL
Una función real es continua en el intervalo [a,b], si es con-
tinua en todo punto de ese intervalo.
Intuitivamente, decimos que una función es continua en un
intervalo, si al representarla gráficamente en ese intervalo
no hay que levantar el lápiz del papel.
Los conceptos de límite y continuidad están íntimamente
relacionados y son la base del concepto de derivada.](https://image.slidesharecdn.com/2-derivadasmaxymin-140424105806-phpapp01/85/2-derivadas-max-y-min-11-320.jpg)








![Prof: René L. Williams G
REGLAS DE DIFERENCIACIÓN
7.
2
)]x(v[
)x´(v)x(u)x(v)x´(u
)x´(f
)x(v
)x(u
)x(f
Derivada de un cuociente.
8. )x´(u)]x(u[n)x´(f)]x(u[)x(f 1nn
u(x) es una función diferenciable de x.
Regla de la cadena.](https://image.slidesharecdn.com/2-derivadasmaxymin-140424105806-phpapp01/85/2-derivadas-max-y-min-22-320.jpg)




![Prof: René L. Williams G
EJEMPLO
1. Dada la función: 1x3x2)x(f 2
Determine:
a) La tasa promedio de cambio en el intervalo [0,5]
13
05
166
m
66y5x
1y0x
b) La derivada.
3x4)x´(f ](https://image.slidesharecdn.com/2-derivadasmaxymin-140424105806-phpapp01/85/2-derivadas-max-y-min-27-320.jpg)



![Prof: René L. Williams G
ESTUDIO DE FUNCIONES
Sea f una función real continua y derivable en el inter-
valo real [a,b].
a) f es creciente en [a,b] ]b,a[x0)x´(f
b) f es decreciente en [a,b] ]b,a[x0)x´(f
c) f es constante en [a,b] ]b,a[x0)x´(f ](https://image.slidesharecdn.com/2-derivadasmaxymin-140424105806-phpapp01/85/2-derivadas-max-y-min-31-320.jpg)

![Prof: René L. Williams G
f(x)
x0 a b c d e f g h i
[a,b[ f(x) es decreciente; f´(x) < 0
]b,d[ f(x) es decreciente; f´(x) < 0
]d,e[ f(x) es decreciente; f´(x) < 0](https://image.slidesharecdn.com/2-derivadasmaxymin-140424105806-phpapp01/85/2-derivadas-max-y-min-33-320.jpg)
![Prof: René L. Williams G
f(x)
x0 a b c d e f g h i
]e,f[ f(x) es creciente; f´(x) > 0
]f,g[ f(x) es creciente; f´(x) > 0
]g,h[ f(x) es decreciente; f´(x) < 0](https://image.slidesharecdn.com/2-derivadasmaxymin-140424105806-phpapp01/85/2-derivadas-max-y-min-34-320.jpg)
![Prof: René L. Williams G
f(x)
x0 a b c d e f g h i
]h,i[ f(x) es decreciente; f´(x) < 0
]i, [ f(x) es creciente; f´(x) > 0](https://image.slidesharecdn.com/2-derivadasmaxymin-140424105806-phpapp01/85/2-derivadas-max-y-min-35-320.jpg)




![Prof: René L. Williams G
f(x)
x0 a b c d e f g h i
En [a,b[ la función es cóncava hacia arriba (+)
En ]b,d[ la función es cóncava hacia abajo (-)
En ]d,f[ la función es cóncava hacia arriba (+)
En ]f,h[ la función es cóncava hacia abajo (-)](https://image.slidesharecdn.com/2-derivadasmaxymin-140424105806-phpapp01/85/2-derivadas-max-y-min-40-320.jpg)


![Prof: René L. Williams G
MÁXIMOS Y MÍNIMOS
PRIMER MÉTODO
a x
[,a]:I
[a,]:I
2
1
Se averigua el signo de f´(x) en cada intervalo, para esto
se toma un valor cualquiera del intervalo y se reemplaza
en f´(x)](https://image.slidesharecdn.com/2-derivadasmaxymin-140424105806-phpapp01/85/2-derivadas-max-y-min-43-320.jpg)
![Prof: René L. Williams G
MÁXIMOS Y MÍNIMOS
PRIMER MÉTODO
a=xenmínimounpresentaf
[+,a]encrecienteesf[+,a]en0>)x´(fSi
[a,]enedecrecientesf[a,∞]en0<)x´(fSi)b
∞⇒∞
∞⇒
• Se decide:
mínimonimáximonihayno
a=xaentornosignodecambiano)x´(fSi)c
máximounpresentafunciónlaa=xenEntonces
[+,a]enedecrecientesf[+,a]en0<)x´(fSi
[a,]encrecienteesf[a,]en0>)x´(fSi)a
∞⇒∞
∞⇒∞](https://image.slidesharecdn.com/2-derivadasmaxymin-140424105806-phpapp01/85/2-derivadas-max-y-min-44-320.jpg)