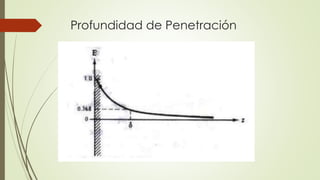
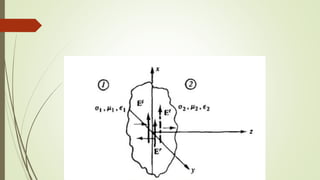
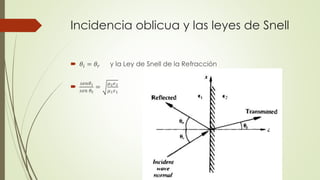
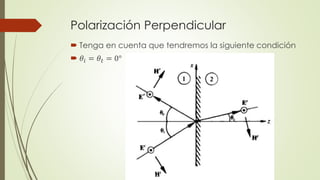
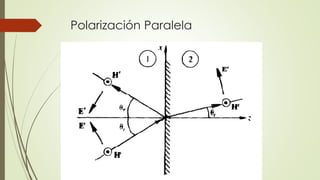
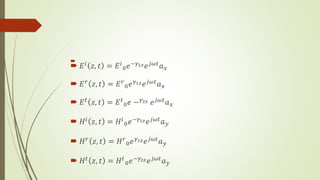El documento describe la profundidad de penetración de ondas electromagnéticas en un medio conductor. Explica que las ondas E y H se atenuan exponencialmente dentro del conductor y se definen cuantitativamente la profundidad de penetración. Luego proporciona ejemplos numéricos de cálculos de profundidad de penetración para diferentes frecuencias y materiales conductores.

1. Ondas Reflejadas
Clase 14
21-Noviembre-2014

2. Profundidad de Penetración
 Las ondas E y H cuando viajan en un medio conductor, son atenuadas por
el factor 푒−훼푧 al avanzar a lo largo de 푧. Esta atenuación es tan rápida que
a menudo las ondas pueden considerarse cero solo a unos pocos
milímetros de avance.
 Considérese que la región 푧 ≥ 0 es un conductor y justo adentro del
conductor, en 푧 = +0, 퐸 tiene magnitud 1V/m. La profundidad de
penetración 훿 , se define como la distancia a partir de la cual 퐸 ha
disminuido a 푒−1 = 0.368 푉/푚.

3. Profundidad de Penetración

4. Profundidad de Penetración
 De esta manera
 훿 =
1
훼
=
1
휋푓휇휎
 Por conveniencia, 푧 = 5훿 se toma a menudo como el
punto donde la función es cero, ya que ahí su valor es
0.0067 o 0.67% del valor inicial.

5. Profundidad de Penetración
 A una frecuencia de 100 MHz en el caso del cobre, la profundidad
de penetración es de 6.61휇푚. Las ondas se atenúan en 0.67% en
5훿 표 33휇푚. Por consiguiente, el termino propagación, cuando se
utiliza conjuntamente con el comportamiento de la onda dentro
de un conductor, es causa de mala interpretación.
 Las Ondas E y H difícilmente se propagan.

6. Profundidad de Penetración
 Como se vera en breve la mayor parte de una onda incidente
sobre la superficie de un conductor se refleja. Sin embargo la
porción que continua dentro del conductor y se atenúa
rápidamente no puede ignorarse completamente, porque da lugar
a una densidad de corriente de conducción 퐽퐶 y a sus
concomitantes perdidas de potencia de tipo óhmico.

7. 

9. 

10. 

11. 

12.  Las cinco ecuaciones anteriores pueden combinarse para producir
las siguientes relaciones dadas en términos de las impedancias
intrínsecas:
푟
퐸0 푖
 퐸0
=
휂2−휂1
휂1+휂2
푟
퐻0 푖
퐻0
=
휂1−휂2
휂1+휂2
 퐸0 푡
퐸0 푖
=
2휂2
휂1+휂2
푡
퐸0 푖
퐻0
=
2휂1
휂1+휂2

13. 

14. 

15. Problema 1
 Las ondas viajeras 퐸 푦 퐻 en el espacio vacío (región 1) inciden
normalmente en la entrecara con un dieléctrico perfecto (región
2), para el que 휖푟 = 3. Compare las magnitudes de las ondas 퐸 푦 퐻
incidentes reflejadas y transmitidas en la entrecara.

16. Solución
 휂1 = 휂0 = 120휋 휂2 =
휇
휖
=
120휋
휖푟
= 217.7
푟
퐸0 푖=
 퐸0
휂2−휂1
휂1+휂2
= −0.268
푟
퐻0 푖
퐻0
=
휂1−휂2
휂1+휂2
= 0.268
 퐸0 푡
퐸0 푖
=
2휂2
휂1+휂2
= 0.732
푡
퐸0 푖
퐻0
=
2휂1
휂1+휂2
= 1.268

17. Incidencia oblicua y las leyes de Snell
 Una onda incidente que se aproxima a un plano entre dos medios
diferentes generalmente dará como resultado una onda
transmitida en la primera. Las normales de las ondas reflejadas y
transmitidas, también se encuentra en el plano de incidencia. El
ángulo de incidencia 휃푖, el ángulo de reflexión 휃푟 y el ángulo de
transmisión están definidas en la siguiente figura.

18. Incidencia oblicua y las leyes de Snell
 휃푖 = 휃푟 y la Ley de Snell de la Refracción
 푠푒푛휃푖
푠푒푛 휃푡
=
휇2휖2
휇1휖1

19. Problema
 Una onda es incidente en un ángulo de 30 ° a partir del aire al
teflón. Calcular el ángulo de la transmisión y repetir con un
intercambio de las regiones.

20. Solución
 Donde
 휇1 = 휇2,
푠푒푛 휃푖
푠푒푛 휃푡
=
푠푒푛30°
푠푒푛 휃푡
=
휖푟2
휖푟1
= 2.1 표 휃푡 = 20.18°
 Del teflón al aire
 푠푒푛30°
푠푒푛 휃푡
=
1
2.1
표 휃푡 = 46.43°

21.  Suponiendo ambos medios tienen la misma permeabilidad, de
propagación desde el medio ópticamente más denso 휖1 > 휖2
tenemos en consecuencia que 휃푡 > 휃푖. A medida que aumenta 휃푖
como el ángulo de incidencia se alcanzará este resultado en 휃푡 =
90°.
 En este ángulo crítico de incidencia, en lugar de una onda que se
transmite en el segundo medio habrá una onda que se propaga a
lo largo de la superficie.

22.  El ángulo critico esta dado por
 휃푐 = 푠푒푛−1 휖푟2
휖푟1

23. Problema
 El ángulo critico para la onda de propagación del teflón al espacio
libre del problema anterior es:
 휃푐 = 푠푒푛−1 1
2.1
= 43.64°

24. Polarización Perpendicular
 La orientación del campo Eléctrico E respecto al plano de
incidencia determina la polarización de la onda entre las dos
diferentes regiones. En la polarización perpendicular E es
perpendicular al plano de incidencia (el 푝푙푎푛표 푥푧 en la figura
siguiente) y es paralelo a la densidad planar (Se utiliza en ciertos
casos teóricos de aplicaciones físicas como los de campo o
corriente eléctrica donde las características de un material se
expresan en densidad por unidad de área).
푟
퐸0 푖
 퐸0
=
휂2푐표푠휃푡−휂1푐표푠휃푖
휂2푐표푠휃푖+휂1푐표푠휃푡
퐸0 푡
퐸0 푖
=
2휂2푐표푠휃푖
휂2푐표푠휃푖−휂1푐표푠휃푡

25. Polarización Perpendicular
 Tenga en cuenta que tendremos la siguiente condición
 휃푖 = 휃푡 = 0°

26. Polarización Paralela
 Para la polarización paralela al vector de campo eléctrico 퐸 se
encuentra totalmente dentro del plano de incidencia al plano
푝푙푎푛표 푥푧 como se muestra en al siguiente figura.
푟
퐸0 푖
 퐸0
=
휂2푐표푠휃푡−휂1푐표푠휃푖
휂1푐표푠휃푖+휂2푐표푠휃푡
퐸0 푡
퐸0 푖
=
2휂2푐표푠휃푖
휂1푐표푠휃푖−휂2푐표푠휃푡

27. Polarización Paralela

28. Polarización Paralela
 En contraste con polarizaciones perpendiculares, si 휇1 = 휇2 habrá
una incidencia particular para la que no hay onda reflejada. Esto
se le conoce como el ángulo de Brewster y esta dado por:
 휃퐵 = 푡푎푛−1 휖2
휖1

29. Problema 3
 El ángulo de Brewster para una onda polarizada paralela que viaja
del aire al vidrio para 휖푟 = 5 es:
 휃퐵 = 푡푎푛−1 5 ≅ 65.91°

30. Problema 4
 ¿ A que frecuencia puede considerarse la tierra un dieléctrico
perfecto si 휎 = 5 × 10−3 푆
푚
, 휇푟 = 1, 푦 휖푟 = 8? ¿Puede suponerse 훼 = 0
a estas frecuencias?
 휃퐵 = 푡푎푛−1 5 ≅ 65.91°

31. Solucion
 Suponemos arbitrariamente que
 휎
휔휖
≤
1
100
esto marca la frecuencia de corte. Entonces
 푓 =
휔
2휋
≥
100휎
2휋휖
= 1.13퐺퐻푧
 Para σ/휔휖 pequeño
 훼 = 휔
휇휖
2
1 +
휎
휔휖
2
− 1

32. Solución
 훼 = 휔
휇휖
2
1 +
휎
휔휖
2
− 1 ≈ 훼 = 휔 휇휖
2
1
2
휎
휔휖
2
= 휎
2
휇
휖
 훼 =
휎
2
휇푟
휖푟
120휋 = 0.333 푁푝/푚
 Así pues no importa que tan alta sea la frecuencia, 훼
será alrededor de 0.333
푁푝
푚
표 푐푎푠푖 3푑퐵/푚

33. Problema 5
 Halle la profundidad de penetración 훿 a una frecuencia de 1.6 Mhz
en el aluminio, donde 38.2
푀푆
푚
푦 휇푟 = 1. También 훾 y la velocidad de
onda U.

34. Problema 6
 Calcule la impedancia intrínseca 휂, la constante de propagación 훾
y la velocidad de la Onda U para un medio conductor en el que
휎 = 58
푀푆
푚
, 휇푟 = 1, a una frecuencia 푓 = 100푀퐻푧

35. Solución
 훾 = 휔휇휎∠45° = 2.14 × 105∠45° 푚−1
 휂 =
휔휇
휎
∠45° = 3.69 × 10−3∠45° Ω
 훼 = 훽 = 1.51 × 105
 훿 =
1
훼
= 6.61 휇푚 푈 = 휔훿 = 4.15 × 103푚/푠

36. Solución
 훿 =
1
휋푓휇휎
= 6.44 × 10−5푚 = 64.4휇푚
 Como 훼 = 훽 = 훿−1
 훾 = 1.55 × 104 + 푗1.55 × 104 = 2.20 × 104∠45°푚−1
 푈 =
휔
훽
= 휔훿 = 647푚/푠

37. Problema 7
 Una onda plana que viaja en la dirección +푧, en el espacio vacío
푧 < 0 incide en forma normal en 푧 = 0 sobre un conductor (푧 > 0)
para que el que 휎 = 61.7
푀푆
푚
, 휇푟 = 1. La onda E en el espacio vacío,
tiene una frecuencia 푓 = 1.5푀퐻푧 y una amplitud de 1V/m. En la
entrecara esta dada por
 퐸 0, 푡 = 1푠푒푛2휋푓푡 푎푦 푉/푚
 Halle 퐻 푧, 푡 푝푎푟푎 푥, 푧 > 0

38. Solución
 Donde se tomara finalmente la parte imaginaria. En el conductor
 훼 = 훽 = 휋푓휇휎 = 휋 1.5 × 106 4휋 × 10−7 61.7 × 106
 훼 = 1.91 × 104
 휂 =
휔휇
휎
∠45° = 4.38 × 10−4푒푗휋/4

39. Solución
 Entonces
퐸푦
−퐻푥
= 휂
휋
4 푎푥 퐴/푚
 퐻 푧, 푡 = −2.28 × 103푒−훼푧푒푗 2휋푓푡−훽푧−
 O tomando la parte imaginaria
 퐻 푧, 푡 = −2.28 × 103푒−훼푧푠푒푛 2휋푓푡 − 훽푧 −
휋
4
푎푥 퐴/푚
 Donde 푓, 훼 푦 훽 los que se dieron antes.

40. Problema 8
 Examine el campo
 퐸 푧, 푡 = 10푠푒푛 휔푡 + 훽푧 푎푥 + 10푐표푠 휔푡 + 훽푧 푎푦
 En el plano 푧 = 0 para 휔푡 = 0,
휋
4
,
휋
2
,
3휋
4
푦 휋

41. Problema 8
Los cálculos se presentan en la tabla 1
흎풕 푬풙 = ퟏퟎ풔풆풏흎풕 푬풚 = ퟏퟎ풄풐풔흎풕 푬 = 푬풙풂풙 + 푬풚풂풚
0 0 0 0
휋/4 10/ 2 10/ 2
10
푎푥 + 푎푦
2
휋/2 10 0 10푎푥
3휋/4 10/ 2 −10/ 2
10
푎푥 + 푎푦
2
휋 −10 −10 10 −푎푦

42. Problema 8
 Como se muestra en la figura siguiente 퐸(푧, 푡) tiene polarización
circular. Además la onda viaja en dirección de −푎푧

43. Potencia y Vector Poyting
 Se escribe la primera ecuación de Maxwell para una región de
conductividad 휎 y luego se toma el producto escalar de 퐸 con cada
término:
 Donde, como es usual, 퐸2 = 퐸 ∙ 퐸. E utiliza la identidad vectorial
 훻 ∙ 퐴 × 퐵 = 퐵 ∙ 훻 × 퐴 − 퐴 ∙ 훻 × 퐵 para cambiar el lado izquierdo de la
ecuación.
훻 × 퐻 = 휎퐸 + 휖
휕퐸
휕푡
퐸 ∙ 훻 × 퐻 = 휎퐸2 + 퐸 ∙ 휖
휕퐸
휕푡

44. Potencia y Vector Poyting
 Por la segunda ecuación de Maxwell, tenemos
 Similarmente,
퐻 ∙ 훻 × 퐸 − 훻 ∙ 퐸 × 퐻 = 휎퐸2 + 퐸 ∙ 휖
휕퐸
휕푡
퐻 ∙ 훻 × 퐸 = 퐻 ∙ −휇
휕퐸
휕푡
= −
휇
2
휕퐻2
휕푡
퐸 ∙ 휖
휕퐸
휕푡
=
휖
2
휕퐸2
휕푡

45. Potencia y Vector Poyting
 Sustituyendo y reordenando términos,
휎퐸2 = −
휖휕퐸2
휕푡
−
휇
2
휕퐻2
휕푡
− 훻 ∙ 퐸 × 퐻
 Si esta igualdad es valida, entonces la integración de sus términos sobre un
volumen general 푣 debe ser valida también
푣
휎퐸2 = −
푣
휖휕퐸2
휕푡
−
휇
2
휕퐻2
휕푡
−
푆
 Donde el ultimo término ha sido convertido a una integral sobre la
superficie de 푣 mediante el teorema de divergencia.
퐸 × 퐻 ∙ 푑푆

46. Potencia y Vector Poyting
 La integral de la izquierda tiene unidades watts y es el termino óhmico
conocido para representar la energía disipada en calor por unidad de
tiempo. Esta energía disipada tiene su fuente en las integrales de la
derecha. Como
ϵ퐸2
2
푦
휇퐻2
2
son las densidades de energía almacenadas
en los campos eléctrico y magnético respectivamente, las derivadas
negativas respecto del tiempo pueden considerarse como una
disminución en esta energía almacenada. Por consiguiente, la integral final
(incluyendo el signo menos) debe ser la tasa de energía que penetra el
volumen desde fuera. Un cambio de signo produce el valor instantáneo de
energía que abandona el volumen:
푃 푡 =
푆
퐸 × 퐻 ∙ 푑푆 =
푆
℘ ∙ 푑푆

47. Potencia y Vector Poyting
 Para ondas planas, la dirección del flujo de energía es la dirección de
propagación. De esta manera, el vector Poynting ofrece una forma una
forma útil y libre del sistema de coordenadas de hallar la dirección de
propagación es conocida. Esto puede tener mucho valor cuando se
examinan ondas incidentes, transmitidas y reflejadas.
℘푝푟표푚 =
1
2
푅푒 퐸 × 퐻∗

48. Potencia y Vector Poyting
 Donde ℘ = 퐸 × 퐻 es el vector de Poyting, tasa instantánea de flujo de
energía por unidad de área en un punto.
 En el producto vectorial que define el vector de Poyting, los campos se
suponen reales. Pero si, 퐸 푦 퐻 se expresan en forman compleja y dependen
en común del tiempo, 푒푗푤푡, entonces el promedio de tiempo de ℘ esta
dado por
 Donde 퐻∗ es la conjugada compleja de H.
 De esto se sigue la potencia compleja del análisis de circuitos, 푆 =
1
2
푉퐼∗, de
la que la potencia es la parte real, 푃 =
1
2
푅푒푉퐼∗
℘푝푟표푚 =
1
2
푅푒 퐸 × 퐻∗