Este documento presenta la transformada de Laplace. Define la transformada de Laplace y explica que mapea funciones con crecimiento exponencial a funciones complejas. Luego enumera algunas propiedades clave de la transformada de Laplace, como que es lineal y cómo se transforman funciones exponenciales, senos y cosenos. Finalmente, incluye una tabla con las transformadas de Laplace de varias funciones comunes.



 = e −st f (t) dt .
0
(Se pide que f sea continua a trozos para que exista la integral.)](https://image.slidesharecdn.com/clase6y7-130219142128-phpapp01/85/Clase-4-320.jpg)
 = e −st f (t) dt, ∀ s > α.
0
Propiedades
La transformada de Laplace tiene las siguientes propiedades:
1 L[αf + βg ] = α L[f ] + β L[g ] para α, β ∈ R.](https://image.slidesharecdn.com/clase6y7-130219142128-phpapp01/85/Clase-5-320.jpg)
 = e −st f (t) dt, ∀ s > α.
0
Propiedades
La transformada de Laplace tiene las siguientes propiedades:
1 L[αf + βg ] = α L[f ] + β L[g ] para α, β ∈ R.
2 L[e −at f (t)](s) = L[f ](s + a) a ∈ R.](https://image.slidesharecdn.com/clase6y7-130219142128-phpapp01/85/Clase-6-320.jpg)
 = e −st f (t) dt, ∀ s > α.
0
Propiedades
La transformada de Laplace tiene las siguientes propiedades:
1 L[αf + βg ] = α L[f ] + β L[g ] para α, β ∈ R.
2 L[e −at f (t)](s)
= L[f ](s + a) a ∈ R.
1 s
3 L[f (at)](s) = L[f (t)] a > 0.
a a](https://image.slidesharecdn.com/clase6y7-130219142128-phpapp01/85/Clase-7-320.jpg)
 = e −st f (t) dt, ∀ s > α.
0
Propiedades
La transformada de Laplace tiene las siguientes propiedades:
1 L[αf + βg ] = α L[f ] + β L[g ] para α, β ∈ R.
2 L[e −at f (t)](s)
= L[f ](s + a) a ∈ R.
1 s
3 L[f (at)](s) = L[f (t)] a > 0.
a a
4 F (s) = L[f ](s) es derivable y F (s) = L[−t f (t)](s).](https://image.slidesharecdn.com/clase6y7-130219142128-phpapp01/85/Clase-8-320.jpg)
 = e −st f (t) dt, ∀ s > α.
0
Propiedades
La transformada de Laplace tiene las siguientes propiedades:
1 L[αf + βg ] = α L[f ] + β L[g ] para α, β ∈ R.
2 L[e −at f (t)](s)
= L[f ](s + a) a ∈ R.
1 s
3 L[f (at)](s) = L[f (t)] a > 0.
a a
4 F (s) = L[f ](s) es derivable y F (s) = L[−t f (t)](s).
5 Si f es continua a trozos y de crecimiento a lo sumo
exponencial, entonces L[f ](s) = s L[f ](s) − f (0).](https://image.slidesharecdn.com/clase6y7-130219142128-phpapp01/85/Clase-9-320.jpg)
 tiene derivadas de todos los ordenes y
´](https://image.slidesharecdn.com/clase6y7-130219142128-phpapp01/85/Clase-10-320.jpg)
 tiene derivadas de todos los ordenes y
´
F (n) (s) = L[(−1)n t n f (t)](s)
.](https://image.slidesharecdn.com/clase6y7-130219142128-phpapp01/85/Clase-11-320.jpg)
 tiene derivadas de todos los ordenes y
´
F (n) (s) = L[(−1)n t n f (t)](s)
.
x
g (x) = f (t) dt tambi´n tiene crecimiento a lo sumo
e
0
L[f ](s) F (s)
exponencial y L[g ](s) = = .
s s](https://image.slidesharecdn.com/clase6y7-130219142128-phpapp01/85/Clase-12-320.jpg)

 = .
s
n!
2 Si f (t) = t n , L[f ](s) = .
s n+1
Γ(a + 1)
3 Si f (t) = t a , L[f ](s) = .
s a+1
1
4 Si f (t) = e at , L[f ](s) = .
s −a
a
5 Si f (t) = sen(at), L[f ](s) = 2 .
s + a2
s
6 Si f (t) = cos(at), L[f ](s) = 2 .
s + a2
sen(at) a
7 Si f (t) = , L[f ](s) = arctan .
t s](https://image.slidesharecdn.com/clase6y7-130219142128-phpapp01/85/Clase-14-320.jpg)
 = .
s
n!
2 Si f (t) = t n , L[f ](s) = .
s n+1
Γ(a + 1)
3 Si f (t) = t a , L[f ](s) = .
s a+1
1
4 Si f (t) = e at , L[f ](s) = .
s −a
a
5 Si f (t) = sen(at), L[f ](s) = 2 .
s + a2
s
6 Si f (t) = cos(at), L[f ](s) = 2 .
s + a2
sen(at) a
7 Si f (t) = , L[f ](s) = arctan .
t s](https://image.slidesharecdn.com/clase6y7-130219142128-phpapp01/85/Clase-15-320.jpg)
 = .
s
n!
2 Si f (t) = t n , L[f ](s) = .
s n+1
Γ(a + 1)
3 Si f (t) = t a , L[f ](s) = .
s a+1
1
4 Si f (t) = e at , L[f ](s) = .
s −a
a
5 Si f (t) = sen(at), L[f ](s) = 2 .
s + a2
s
6 Si f (t) = cos(at), L[f ](s) = 2 .
s + a2
sen(at) a
7 Si f (t) = , L[f ](s) = arctan .
t s](https://image.slidesharecdn.com/clase6y7-130219142128-phpapp01/85/Clase-16-320.jpg)
 = .
s
n!
2 Si f (t) = t n , L[f ](s) = .
s n+1
Γ(a + 1)
3 Si f (t) = t a , L[f ](s) = .
s a+1
1
4 Si f (t) = e at , L[f ](s) = .
s −a
a
5 Si f (t) = sen(at), L[f ](s) = 2 .
s + a2
s
6 Si f (t) = cos(at), L[f ](s) = 2 .
s + a2
sen(at) a
7 Si f (t) = , L[f ](s) = arctan .
t s](https://image.slidesharecdn.com/clase6y7-130219142128-phpapp01/85/Clase-17-320.jpg)
 = .
s
n!
2 Si f (t) = t n , L[f ](s) = .
s n+1
Γ(a + 1)
3 Si f (t) = t a , L[f ](s) = .
s a+1
1
4 Si f (t) = e at , L[f ](s) = .
s −a
a
5 Si f (t) = sen(at), L[f ](s) = 2 .
s + a2
s
6 Si f (t) = cos(at), L[f ](s) = 2 .
s + a2
sen(at) a
7 Si f (t) = , L[f ](s) = arctan .
t s](https://image.slidesharecdn.com/clase6y7-130219142128-phpapp01/85/Clase-18-320.jpg)
 = .
s
n!
2 Si f (t) = t n , L[f ](s) = .
s n+1
Γ(a + 1)
3 Si f (t) = t a , L[f ](s) = .
s a+1
1
4 Si f (t) = e at , L[f ](s) = .
s −a
a
5 Si f (t) = sen(at), L[f ](s) = 2 .
s + a2
s
6 Si f (t) = cos(at), L[f ](s) = 2 .
s + a2
sen(at) a
7 Si f (t) = , L[f ](s) = arctan .
t s](https://image.slidesharecdn.com/clase6y7-130219142128-phpapp01/85/Clase-19-320.jpg)
 = .
s
n!
2 Si f (t) = t n , L[f ](s) = .
s n+1
Γ(a + 1)
3 Si f (t) = t a , L[f ](s) = .
s a+1
1
4 Si f (t) = e at , L[f ](s) = .
s −a
a
5 Si f (t) = sen(at), L[f ](s) = 2 .
s + a2
s
6 Si f (t) = cos(at), L[f ](s) = 2 .
s + a2
sen(at) a
7 Si f (t) = , L[f ](s) = arctan .
t s](https://image.slidesharecdn.com/clase6y7-130219142128-phpapp01/85/Clase-20-320.jpg)
 resulta:
Γ(b + 1)
1 Si f (t) = e at t b , L[f ](s) = .
(s − a)b+1
b
2 Si f (t) = e at sen(bt), L[f ](s) = .
(s − a)2 + b 2
s −a
3 Si f (t) = e at cos(bt), L[f ](s) = .
(s − a)2 + b 2
e at − e −at a
4 Si f (t) = senh(at) = , L[f ](s) = 2 .
2 s − a2
e at + e −at s
5 Si f (t) = cosh(at) = , L[f ](s) = 2 .
2 s − a2](https://image.slidesharecdn.com/clase6y7-130219142128-phpapp01/85/Clase-21-320.jpg)
 resulta:
Γ(b + 1)
1 Si f (t) = e at t b , L[f ](s) = .
(s − a)b+1
b
2 Si f (t) = e at sen(bt), L[f ](s) = .
(s − a)2 + b 2
s −a
3 Si f (t) = e at cos(bt), L[f ](s) = .
(s − a)2 + b 2
e at − e −at a
4 Si f (t) = senh(at) = , L[f ](s) = 2 .
2 s − a2
e at + e −at s
5 Si f (t) = cosh(at) = , L[f ](s) = 2 .
2 s − a2](https://image.slidesharecdn.com/clase6y7-130219142128-phpapp01/85/Clase-22-320.jpg)
 resulta:
Γ(b + 1)
1 Si f (t) = e at t b , L[f ](s) = .
(s − a)b+1
b
2 Si f (t) = e at sen(bt), L[f ](s) = .
(s − a)2 + b 2
s −a
3 Si f (t) = e at cos(bt), L[f ](s) = .
(s − a)2 + b 2
e at − e −at a
4 Si f (t) = senh(at) = , L[f ](s) = 2 .
2 s − a2
e at + e −at s
5 Si f (t) = cosh(at) = , L[f ](s) = 2 .
2 s − a2](https://image.slidesharecdn.com/clase6y7-130219142128-phpapp01/85/Clase-23-320.jpg)
 resulta:
Γ(b + 1)
1 Si f (t) = e at t b , L[f ](s) = .
(s − a)b+1
b
2 Si f (t) = e at sen(bt), L[f ](s) = .
(s − a)2 + b 2
s −a
3 Si f (t) = e at cos(bt), L[f ](s) = .
(s − a)2 + b 2
e at − e −at a
4 Si f (t) = senh(at) = , L[f ](s) = 2 .
2 s − a2
e at + e −at s
5 Si f (t) = cosh(at) = , L[f ](s) = 2 .
2 s − a2](https://image.slidesharecdn.com/clase6y7-130219142128-phpapp01/85/Clase-24-320.jpg)
 resulta:
Γ(b + 1)
1 Si f (t) = e at t b , L[f ](s) = .
(s − a)b+1
b
2 Si f (t) = e at sen(bt), L[f ](s) = .
(s − a)2 + b 2
s −a
3 Si f (t) = e at cos(bt), L[f ](s) = .
(s − a)2 + b 2
e at − e −at a
4 Si f (t) = senh(at) = , L[f ](s) = 2 .
2 s − a2
e at + e −at s
5 Si f (t) = cosh(at) = , L[f ](s) = 2 .
2 s − a2](https://image.slidesharecdn.com/clase6y7-130219142128-phpapp01/85/Clase-25-320.jpg)
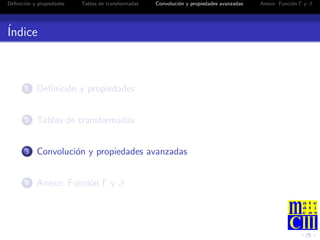



 = L[f ](s) · L[g ](s).](https://image.slidesharecdn.com/clase6y7-130219142128-phpapp01/85/Clase-30-320.jpg)
 = L[f ](s) · L[g ](s).
0 si t < 0
Si definimos la funci´n de salto H(t) =
o entonces
1 si t ≥ 0
H(t − a) es la “misma” funci´n pero con el salto en t = a.
o](https://image.slidesharecdn.com/clase6y7-130219142128-phpapp01/85/Clase-31-320.jpg)
 = L[f ](s) · L[g ](s).
0 si t < 0
Si definimos la funci´n de salto H(t) =
o entonces
1 si t ≥ 0
H(t − a) es la “misma” funci´n pero con el salto en t = a.
o
Transformada y exponenciales
Dada f (t) continua a trozos en [0, ∞) y de crecimiento a lo sumo
exponencial, se tiene:
(a) L[f (t − a)H(t − a)](s) = e −as · L[f ](s).
(b) L[f (t)H(t − a)](s) = e −as · L[f (t + a)](s).](https://image.slidesharecdn.com/clase6y7-130219142128-phpapp01/85/Clase-32-320.jpg)