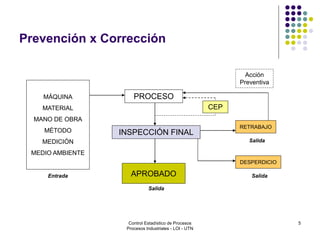
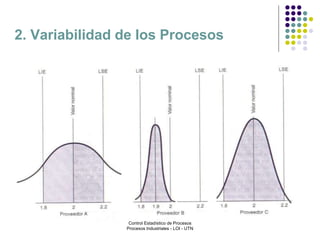
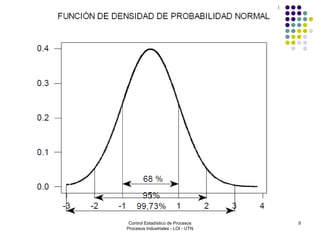
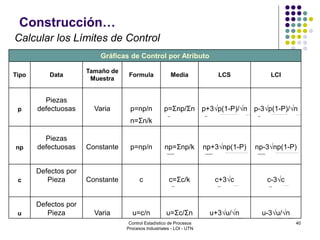
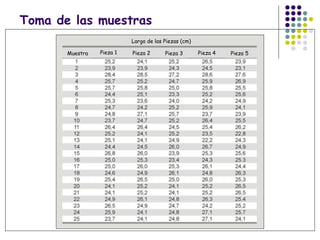
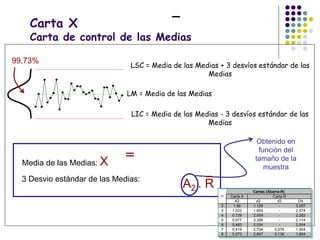
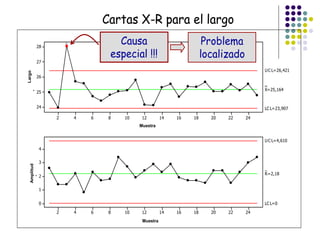
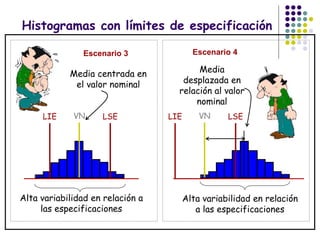
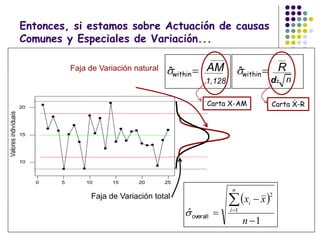
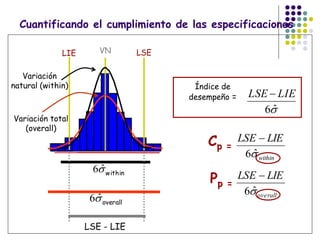
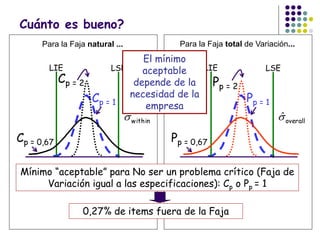
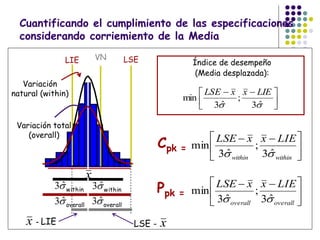
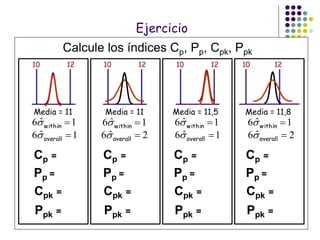
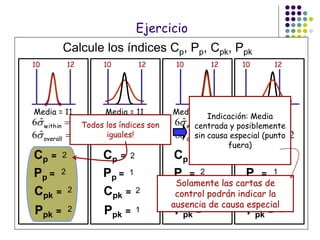
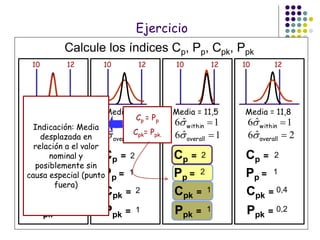
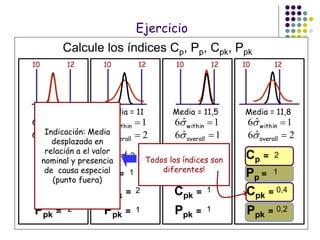
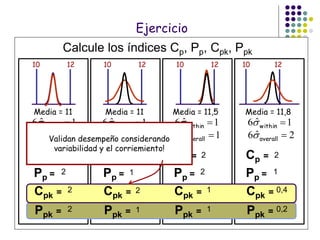
El documento aborda el control estadístico de procesos (CEP) en la industria, destacando su importancia en la prevención de variaciones y la mejora de la calidad de productos a través de técnicas estadísticas y gráficos de control. Se describen las causas de variación en los procesos, diferenciando entre causas comunes y especiales, y se presentan diferentes tipos de gráficos de control para identificar y gestionar estas variaciones. Además, se explica cómo interpretar estos gráficos para asegurar que los procesos se mantengan dentro de límites de control adecuados.