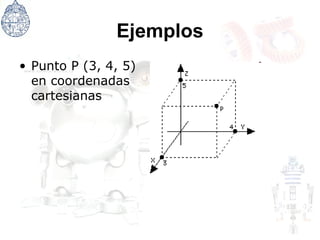
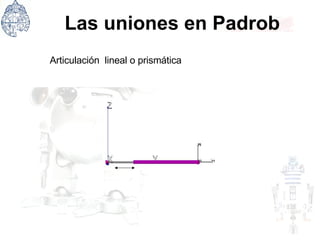
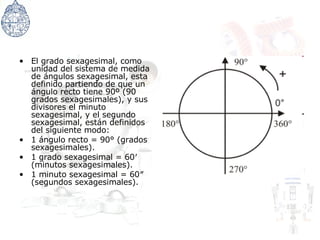
Este documento presenta conceptos básicos de geometría analítica y sistemas de coordenadas. Explica el plano cartesiano y las coordenadas cartesianas, y cómo se pueden usar para definir la posición de un punto en el espacio. También introduce conceptos como grados de libertad, tipos de articulaciones mecánicas, y unidades para medir ángulos como grados, minutos, segundos y radianes.

1. Conceptos básicos teóricos Curso de Padrob

2. Resumen En esta unidad aprenderemos/repasaremos los siguientes conceptos: Nociones de geometría analítica y sistemas coordenados Medidas angulares

3. Geometría analítica La geometría analítica es una herramienta matemática que permite estudiar las figuras geométricas introduciendo un sistema coordenado, de tal manera de que dada una ecuación se determina su gráfica y recíprocamente, dada una gráfica, deducir su ecuación. Parte del concepto de plano cartesiano, y es lo suficientemente poderosa (y sencilla a la vez) como para ser usada en dos dimensiones (plano) y tres dimensiones (espacio)

4. Definición El plano cartesiano está determinado por dos rectas llamadas ejes de coordenadas: El eje horizontal recibe el nombre de eje x o de abscisas. El eje vertical recibe el nombre de eje y o de ordenadas. En ambos ejes se pueden representar los números enteros y se cruzan en el cero.

5. Sistemas de Coordenadas Un sistema de coordenadas se puede definir como un conjunto de valores que permiten definir inequívocamente la posición de cualquier punto en el espacio En aplicaciones matemáticas y físicas se usan sistemas de coordenadas ortogonales Cuando se habla de “sistema de referencia”, se debe asociar a un punto de referencia y un sistema de coordendas Por lo general, se acostumbra denominar a un punto genérico con la letra “P”, y a continuación sus coordenadas

6. Coordenadas cartesianas El sistema de coordenadas cartesianas es aquel formado por dos ejes en el plano o tres en el espacio, mutuamente perpendiculares y que se cortan en el origen. En el plano, las coordenadas cartesianas o rectangulares x e y se denominan respectivamente abscisa y ordenada Notación: P (x,y,z)

7. Ejemplos Punto P (3, 4, 5) en coordenadas cartesianas

8. El módulo (distancia entre puntos) El módulo o distancia entre puntos, es la longitud del segmento de recta que une los puntos Para comenzar a estudiar esto, interesa saber sobre todo la distancia entre el origen y el punto en cuestión; para ello se debe aplicar el teorema de pitágoras En coordenadas cartesianas P (x,y,z):

9. Usando Padrob… La aplicación de la geometría analítica ayuda a determinar posiciones de elementos en el espacio ¿Imagina cómo darle ubicación al extremo de este brazo robótico dibujado en Padrob?

10. Se observa que el brazo está manipulando un objeto de forma cúbica con sus tenazas, está en el suelo, por ende z=0, como se apoya sobre el eje y, x=0, y la distancia “y” es el valor que aparece “d”, por ello, en coordenadas cartesianas su posición sería (0, d, 0) ¿lo calculó igual? Usando Padrob… y d

11. Acotación importante Además de ubicar el extremo del brazo robótico mediante la posición (x,y,z), se debe pensar en la orientación del objeto Observa los dos gráficos siguientes: y y

12. Acotación importante Aunque la posición del cubo es la misma, ciertamente es distinto que la pequeña pieza negra que tiene soldada apunte en “+y” que en “-y”

13. Esto implica que además de la ubicación del extremo de una articulación, hay que pensar en su orientación también

14. Los grados de libertad Un cuerpo aislado en el espacio puede desplazarse libremente en un movimiento que se puede descomponer en 3 rotaciones y 3 traslaciones geométricas independientes (traslaciones y rotaciones respecto de ejes fijos en las 3 direcciones de una base referida a nuestro espacio de tres dimensiones).

15. Los grados de libertad Es por las ideas anteriormente discutidas que, por ejemplo, los robots tienen distintos tipos de articulaciones: torsional, rotacional y lineal (o prismática)

16. Las uniones en Padrob Articulación lineal o prismática

17. Las uniones en Padrob Articulación Rotacional

18. La manipulación mecánica Articulación Torsional

19. Medidas angulares Se denomina ángulo en el plano a la porción de plano comprendida entre dos semirrectas con un origen común denominado vértice. Otra concepción de ángulo dice que éste es la figura formada por dos rayos con origen común. Con cualquiera de estos dos conceptos, un ángulo determina una superficie abierta (subconjunto abierto de puntos del plano), al estar definido por dos semirrectas, la medida de ángulos es la medida de la abertura de estas semirrectas, que se denomina medida del ángulo.

20. El grado sexagesimal, como unidad del sistema de medida de ángulos sexagesimal, esta definido partiendo de que un ángulo recto tiene 90º (90 grados sexagesimales), y sus divisores el minuto sexagesimal, y el segundo sexagesimal, están definidos del siguiente modo: 1 ángulo recto = 90° (grados sexagesimales). 1 grado sexagesimal = 60′ (minutos sexagesimales). 1 minuto sexagesimal = 60″ (segundos sexagesimales).

21. El radián es la unidad del ángulo plano en el Sistema Internacional de Unidades conocido por SI. Pese a que inicialmente fue clasificado, junto al estereorradián, como unidad suplementaria, dicha clasificación se considera obsoleta, atribuyéndose a ambas la categoría de unidad derivada

22. En Padrob… Las medidas angulares deben ser entregadas en radianes

23. Ejercicios Determine cuánto es en radianes: 180º 90º 60º 37º 22º