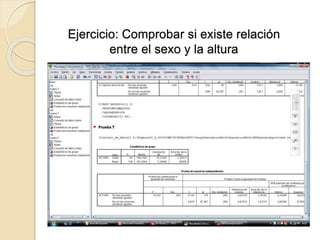
Este documento resume los pasos para aplicar la prueba t de Student a dos conjuntos de datos. Explica que la prueba requiere que al menos una variable sea cuantitativa y siga una distribución normal, y que se debe comprobar la igualdad de varianzas. Luego, presenta dos ejemplos de aplicación de la prueba t de Student para comprobar si existe una relación entre variables como el sexo y la altura, o el sexo y el número de cigarrillos fumados al día. En ambos casos, la prueba encontró una diferencia estadístic

1. Ejercicio T de Student
Amanda Núñez Granado
1º enfermería Macarena grupo A (subgrupo 3)
Estadística y TICs

2. Características T de
Student
 Antes de comenzar con los ejercicios hacer unas
aclaraciones sobre la T de Student.
 Se trata de una prueba paramétrica que cuenta
con una serie de condiciones de aplicabilidad.
Estas son:
-Siempre se utilizan con al menos una variable
cuantitativa (de intervalo o razón en SPSS)
-Exigen que una de las variables siga una
distribución normal. La variable cuantitativa se
somete al test de Kolmogorov ( si N>50) o de
Shapiro( si N<50) para comprobarlo.
-Homocedasticidad o igualdad de varianzas.

3. Ejercicio: Comprobar si existe relación
entre el sexo y la altura

4. Pasos
 Observamos que hay una variable cuantitativa( la
altura) y otra dicotómica ( el sexo). La variable
cuantitativa ha sido sometida a la prueba de la
normalidad mediante el test de Kolmogorov-
Smirnov ( porque N=172>50) y tras establecer la
hipótesis nula: sigue la distribución normal, como la
significación obtenida es mayor a 0,05 ,se acepta
Ho , lo que quiere decir que la altura si sigue una
distribución normal. Vemos que se cumplen las
condiciones de aplicabilidad de la T de Student.
 Después como se trata de dos muestras
independientes, tenemos que observar en primer
lugar la prueba de Levene en la que contrastamos
si se asume o no la Ho de igualdad de varianzas.
Ho= igualdad de varianzas

5.  Como en la prueba de Levene observamos que la
significación es de 0,02 que es < a 0,05 , se acepta
Ho , es decir, se asume la igualdad de varianza.
 En segundo lugar observamos la fila “ se asumen
varianzas iguales” y vemos que la significación
lateral para la prueba T( con gl= 170) es 0,000 que
es menor a 0,05 por lo que se rechaza la hipótesis
nula, que establecía que no hay diferencia entre el
sexo y la altura.

6.  Solución: Existe una diferencia
estadísticamente
significativa(p=0,000) en la relación
entre la altura y el sexo.

7. Otro ejercicio: ¿Existe relación entre el
sexo y el numero de cigarrillos que se fuma
al día?

8. Pasos
-Observamos que hay una variable cuantitativa( nº de cigarrillos
al día) y otra dicotómica( el sexo). Al igual que en el ejercicio
anterior , la variable cuantitativa es sometida a la prueba de la
normalidad mediante el test de Shapiro( porque N<50). Una
vez establecida Ho : sigue la distribución normal, observamos
que la significación obtenida es 0,519>0,05 , por lo que se
acepta Ho y podemos decir que esta variable si sigue una
distribución normal. Vemos por tanto, que se cumplen las
condiciones de aplicabilidad de la T de Student.
-En primer lugar , al tratarse de dos muestras independientes
,observamos la prueba de Levene; con la que comprobamos si
se asume o no igualdad de varianza.
Ho: igualdad de varianza

9.  Como en la prueba de Levene obtenemos una
significación de 0,519, que es > a 0,05 se acepta Ho
, es decir, se asume igualdad de varianza.
 En segundo lugar observamos la fila” se asumen
varianzas iguales” y se observa que la significación
bilateral para la prueba T( con gl=30) es 0,357 <
que 0,05 por lo que se rechaza la hipótesis nula, es
decir, hay diferencia significativa entre el sexo y el
número de cigarros que se fuma al día.

10.  Solución: Existe una diferencia
estadísticamente significativa en la
relación entre el sexo y el número de
cigarrillos que se fuma al día.