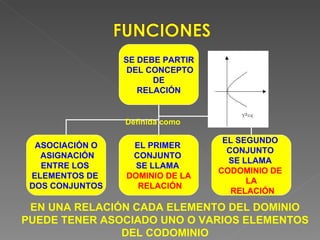
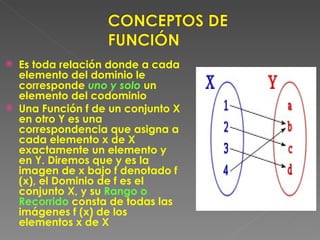
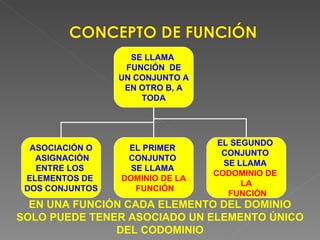
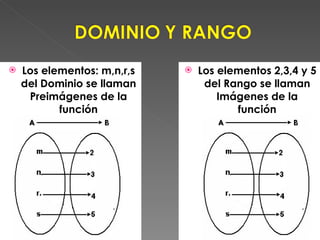
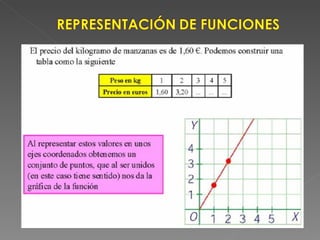
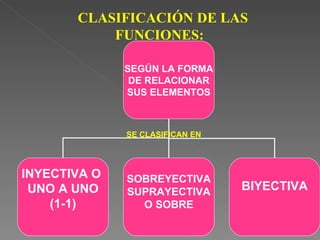
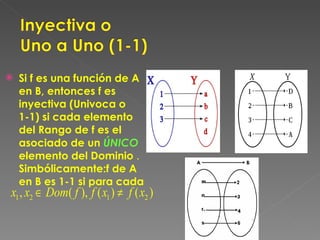
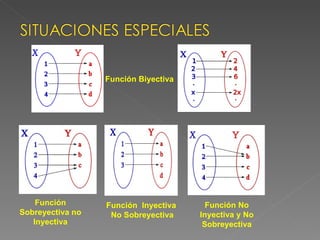
El documento define las relaciones y funciones, y explica las diferencias entre ellas. Explica que una relación asocia elementos de dos conjuntos donde cada elemento del dominio puede estar asociado con más de un elemento del codominio, mientras que una función asocia elementos de dos conjuntos donde cada elemento del dominio solo puede estar asociado con un único elemento del codominio. También clasifica las funciones como inyectivas, sobreyectivas o biyectivas dependiendo de si la asociación entre los elementos es única o no, y cubre otros conceptos clave como el dominio, codominio

1. EN UNA RELACIÓN CADA ELEMENTO DEL DOMINIO PUEDE TENER ASOCIADO UNO O VARIOS ELEMENTOS DEL CODOMINIO SE DEBE PARTIR DEL CONCEPTO DE RELACIÓN ASOCIACIÓN O ASIGNACIÓN ENTRE LOS ELEMENTOS DE DOS CONJUNTOS EL PRIMER CONJUNTO SE LLAMA DOMINIO DE LA RELACIÓN EL SEGUNDO CONJUNTO SE LLAMA CODOMINIO DE LA RELACIÓN Definida como

2. Es toda relación donde a cada elemento del dominio le corresponde uno y solo un elemento del codominio Una Función f de un conjunto X en otro Y es una correspondencia que asigna a cada elemento x de X exactamente un elemento y en Y. Diremos que y es la imagen de x bajo f denotado f (x), el Dominio de f es el conjunto X, y su Rango o Recorrido consta de todas las imágenes f (x) de los elementos x de X

3. EN UNA FUNCIÓN CADA ELEMENTO DEL DOMINIO SOLO PUEDE TENER ASOCIADO UN ELEMENTO ÚNICO DEL CODOMINIO SE LLAMA FUNCIÓN DE UN CONJUNTO A EN OTRO B, A TODA ASOCIACIÓN O ASIGNACIÓN ENTRE LOS ELEMENTOS DE DOS CONJUNTOS EL PRIMER CONJUNTO SE LLAMA DOMINIO DE LA FUNCIÓN EL SEGUNDO CONJUNTO SE LLAMA CODOMINIO DE LA FUNCIÓN

4. Dominio : Es el primer conjunto que intervienen en la función (conjunto A o X) también se le llama conjunto de partida. Se denota por DOM(f) Codominio : Es el segundo conjunto que intervienen en la función (conjunto B o Y) también se le llama conjunto de Llegada. Se denota por COD(f) . Rango : los elementos de B que están asociados con los elementos de A forman otro conjunto denominado Rango o Recorrido de la Función. Se denota por Ran(f) Imagen : si x es un elemento del Dominio, la notación f (x) se utiliza para designar el elemento en el recorrido que corresponde a X en la función f, y se denomina Imagen de X. NOTA: TODA FUNCIÓN ES UNA RELACIÓN, PERO NO TODA RELACIÓN ES UNA FUNCIÓN.

5. Los elementos: m,n,r,s del Dominio se llaman Preimágenes de la función Los elementos 2,3,4 y 5 del Rango se llaman Imágenes de la función

6. POR FÓRMULAS O ECUACIONES POR TABLAS DE VALORES POR DIAGRAMAS SAGITALES POR DIAGRAMAS CARTESIANOS POR EXTENSIÓN POR COMPRENSIÒN

8. CLASIFICACIÓN DE LAS FUNCIONES: SE CLASIFICAN EN SEGÚN LA FORMA DE RELACIONAR SUS ELEMENTOS INYECTIVA O UNO A UNO (1-1) SOBREYECTIVA SUPRAYECTIVA O SOBRE BIYECTIVA

9. Si f es una función de A en B, entonces f es inyectiva (Univoca o 1-1) si cada elemento del Rango de f es el asociado de un ÚNICO elemento del Dominio . Simbólicamente:f de A en B es 1-1 si para cada

10. Una función f es sobreyectiva si y solo si todo elemento del Codominio es imagen, al menos, de un elemento del Dominio. También así: una función f es sobre si el Rango es el mismo Codominio. O sea: f de A en B es Sobreyectiva si y solo si Ran(f)=Cod(f)

11. Una función es biyectiva si es inyectiva y sobreyectiva a la vez, es decir: f: A -> B es Biyectiva si y solo si, f es 1-1 y sobreyectiva a la vez.

12. Inyectiva o Uno a Uno (1-1): Si f es una función de X en Y, entonces f es inyectiva (Univoca o 1-1) si cada elemento del Rango de f es el asociado de un UNICO elemento del Dominio. 2. Sobreyectiva: Una función f es sobreyectiva si y solo si todo elemento del Codominio, es imagen al menos de un elemento del Dominio. También así: una función f es sobre si el Rango es el mismo Codominio. Ran(f)=Cod(f) 3. Biyectiva: Una función es biyectiva si es inyectiva y sobreyectiva a la vez, es decir: f: A -> B es Biyectiva si y solo si, f es 1- 1 y sobre a la vez

13. Función Biyectiva Función No Inyectiva y No Sobreyectiva Función Sobreyectiva no Inyectiva Función Inyectiva No Sobreyectiva

14. CLASIFICACIÓN DE LAS FUNCIONES SEGÚN SU ESTRUCTURA O SU CONFORMACIÒN ALGEBRAICAS TRASCENDENTES ESPECIALES SE CLASIFICAN EN