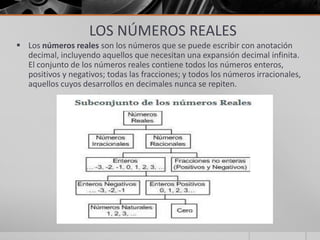
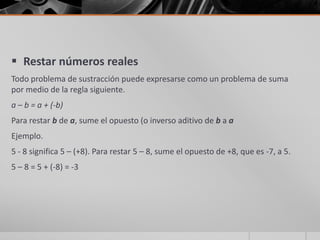
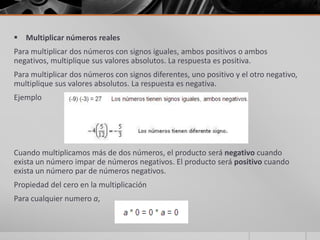
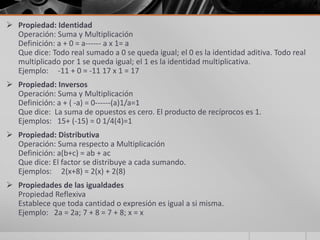
Este documento trata sobre los sistemas de números reales. Explica que los números reales incluyen números enteros, fracciones y números irracionales. Clasifica los números reales como racionales e irracionales, y también como algebraicos y trascendentes. Describe operaciones básicas como suma, resta, multiplicación y división con números reales, así como propiedades importantes como conmutatividad, asociatividad y distributividad. Finalmente, introduce conceptos como axiomas de orden, inecuaciones e valor absoluto.

1. UNIVERSIDAD TECNOLÓGICA
EQUINOCCIAL
MATEMÁTICA SUPERIOR
SISTEMA DE LOS NÚMEROS REALES
REALIZADO POR: RAMIRO FABIÁN DÍAZ RÍOS
PERIODO ACADÉMICO MARZO-AGOSTO 2013

2. LOS NÚMEROS REALES
 Los números reales son los números que se puede escribir con anotación
decimal, incluyendo aquellos que necesitan una expansión decimal infinita.
El conjunto de los números reales contiene todos los números enteros,
positivos y negativos; todas las fracciones; y todos los números irracionales,
aquellos cuyos desarrollos en decimales nunca se repiten.

3. CLASIFICACIÓN DE LOS NÚMEROS REALES
Un número real puede ser un numero racional o un numero irracional. Los números racionales son
aquellos que pueden expresarse como el cociente de dos números enteros, tal como 3/4, -21/3, 5, 0,
1/2, mientras que los irracionales son todos los demás. Los números racionales también pueden
describirse como aquellos cuya representación decimal es eventualmente periódica, mientras que los
irracionales tienen una expansión decimal aperiódica:
Ejemplos 1/4 = 0,250000... Es un número racional puesto que es periódico a partir del tercer número
decimal. 5/7 = 0,7142857142857142857.... Es racional y tiene un período de longitud 6 (repite
714285).
es irracional y su expansión decimal es aperiódica.
Otra forma de clasificar los números reales es en algebraicos y transcendentes. Un número es
algebraico si existe un polinomio de coeficientes racionales que lo tiene por raíz y es trascendente en
caso contrario. Obviamente, todos los números racionales son algebraicos: si es un número racional,
con p entero y q natural, entonces es raíz del de la ecuación qx=p. Sin embargo, no todos los números
algebraicos son racionales.
Ejemplos
El número es algebraico puesto que es la raíz del polinomio

4. OPERACIONES CON NÚMEROS REALES
Sumar números reales
Para sumar dos números con el mismo signo (ambos positivos o ambos negativos)
Sume sus valores absolutos y coloque el mismo signo común antes de la suma. La suma de dos números
positivos será un número positivo, y la suma de dos números negativos será un número negativo.
Ejemplo. -5 + (-9)
Solución: Como ambos números que se suman son negativos, la suma será negativa.
Para determinar la suma, sume los valores absolutos de estos números y coloque un signo negativo antes
del valor.
Para sumar dos números con signos diferentes (uno positivo y el otro negativo)
Reste el valor absoluto menor del valor absoluto mayor. La respuesta tiene el signo del número con el
valor absoluto más grande. La suma de un número positivo y un número negativo puede ser positiva,
negativa o cero, el signo de la respuesta será el mismo signo que el numero con mayor valor absoluto.
Ejemplo. 3 + (-8) Como los números que se suman son de signos opuestos, restamos el valor absoluto
más pequeño del valor absoluto mayor. Primero tomamos cada valor absoluto.
Ahora determinamos la diferencia, 8 – 3 = 5. El número -8 tiene un valor absoluto mayor que el número 3,
por lo que la suma es negativa.
3 + (-8) = -5

5.  Restar números reales
Todo problema de sustracción puede expresarse como un problema de suma
por medio de la regla siguiente.
a – b = a + (-b)
Para restar b de a, sume el opuesto (o inverso aditivo de b a a
Ejemplo.
5 - 8 significa 5 – (+8). Para restar 5 – 8, sume el opuesto de +8, que es -7, a 5.
5 – 8 = 5 + (-8) = -3

6.  Multiplicar números reales
Para multiplicar dos números con signos iguales, ambos positivos o ambos
negativos, multiplique sus valores absolutos. La respuesta es positiva.
Para multiplicar dos números con signos diferentes, uno positivo y el otro negativo,
multiplique sus valores absolutos. La respuesta es negativa.
Ejemplo
Cuando multiplicamos más de dos números, el producto será negativo cuando
exista un número impar de números negativos. El producto será positivo cuando
exista un número par de números negativos.
Propiedad del cero en la multiplicación
Para cualquier numero a,

7.  Dividir números reales
Para dividir dos números con signos iguales, ambos positivos o ambos
negativos, divida sus valores absolutos. La respuesta es positiva.
Para dividir dos números con signos diferentes, uno positivo y el otro negativo,
divida sus valores absolutos. La respuesta es negativa.
Ejemplos.
Cuando el denominador de una fracción es un numero negativo, por lo común
reescribimos la fracción con un denominador positivo. Para hacerlo, usamos el
hecho siguiente.

8. PROPIEDADES
Propiedades de los números reales
 Propiedad: Conmutativa
Operación: Suma y Resta
Definición: a+b = b+a
Que dice:
El orden al sumar o multiplicar reales no afecta el resultado.
Ejemplo: 2+8 = 8+2 5(-3) = ( -3)5
 Propiedad: Asociativa
Operación: Suma y Multiplicación
Definición: a+(b+c)=(a+b)+c------ a(bc) = (ab)c
Que dice:
Puedes hacer diferentes asociaciones al sumar o multiplicar reales y no se afecta
el resultado.
Ejemplo: 7+(6+1)=(7+6)+1 -2(4x7)= (-2x4)7

9.  Propiedad: Identidad
Operación: Suma y Multiplicación
Definición: a + 0 = a------ a x 1= a
Que dice: Todo real sumado a 0 se queda igual; el 0 es la identidad aditiva. Todo real
multiplicado por 1 se queda igual; el 1 es la identidad multiplicativa.
Ejemplo: -11 + 0 = -11 17 x 1 = 17
 Propiedad: Inversos
Operación: Suma y Multiplicación
Definición: a + ( -a) = 0------(a)1/a=1
Que dice: La suma de opuestos es cero. El producto de recíprocos es 1.
Ejemplos: 15+ (-15) = 0 1/4(4)=1
 Propiedad: Distributiva
Operación: Suma respecto a Multiplicación
Definición: a(b+c) = ab + ac
Que dice: El factor se distribuye a cada sumando.
Ejemplos: 2(x+8) = 2(x) + 2(8)
 Propiedades de las igualdades
Propiedad Reflexiva
Establece que toda cantidad o expresión es igual a si misma.
Ejemplo: 2a = 2a; 7 + 8 = 7 + 8; x = x

10.  Propiedad Simétrica
Consiste en poder cambiar el orden de los miembros sin que la igualdad se altere.
Ejemplo: Si 39 + 11 = 50, entonces 50 = 39 + 11
Si a - b = c, entonces c = a - b
Si x = y, entonces y = x
 Propiedad Transitiva
Enuncia que si dos igualdades tienen un miembro en común los otros dos
miembros también son iguales.
Ejemplo:
Si 4 + 6 = 10 y 5 + 5 = 10, entonces 4 + 6 = 5 +...

11. AXIOMAS DE ORDEN
Para que todos los procedimientos matemáticos usados sean válidos se debe partir de una base que
respalde cada procedimiento, cada paso lógico usado, y debe, en consecuencia, demostrarse cada
afirmación no trivial. Son estas demostraciones los pilares fundamentales de toda rama de las
matemáticas, ya que sin ellos puede ponerse en duda la veracidad de cualquier afirmación.
Las afirmaciones a las que se hace referencia se llaman axiomas. Serán, por lo tanto, afirmaciones
que se aceptan como verdaderas debido a su trivialidad, pudiendo en ocasiones ser demostradas
cuando no lo son.
El otro tipo de afirmaciones a las que se hace referencia diciendo: "afirmación no trivial", son los
teoremas, que son ya, afirmaciones no tan triviales y muchas veces poco intuitivas. Estas
afirmaciones deben ser demostradas usando los axiomas u otros teoremas ya demostrados. Una
consecuencia inmediata de un teorema se llamará corolario.
Hay tres tipos de axiomas:
 Los axiomas algebraicos
 Los axiomas de orden
 El axioma topológico.
El primero, trata de las propiedades de suma, resta, multiplicación y división; el segundo establece
un orden para los elementos de cada conjunto dado; el tercero trata sobre la noción de continuidad.

12. INECUACIONES ELEMENTALES
 En matemática, una inecuación es una desigualdad algebraica en la que
aparecen una o más incógnitas en los miembros de la desigualdad. Si la
desigualdad es del tipo o se denomina inecuación en sentido estricto y si es
del tipo o se denomina inecuación en sentido amplio.
Del mismo modo en que se hace la diferencia entre igualdad y ecuación, una
inecuación que es válida para todas las variables se llama inecuación
incondicional y las que son válidas solo para algunos valores de las variables se
conocen como inecuaciones condicionales. Los valores que verifican la
desigualdad, son sus soluciones.
 Ejemplo de inecuación incondicional: .
 Ejemplo de inecuación condicional: .

13. VALOR ABSOLUTO
 En matemática, el valor absoluto o módulo de un numero real es su valor
numérico sin tener en cuenta su signo, sea este positivo (+) o negativo (-). Así,
por ejemplo, 3 es el valor absoluto de 3 y de -3.
El valor absoluto está relacionado con las nociones de magnitud, distancia y
norma en diferentes contextos matemáticos y físicos. El concepto de valor absoluto
de un número real puede generalizarse a muchos otros objetos matemáticos, como
son los cuaterniones, anillos ordenados, cuerpos o espacios vectoriales.