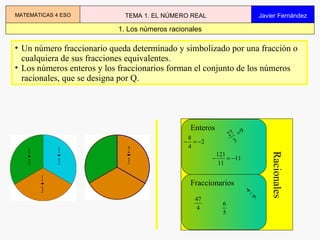
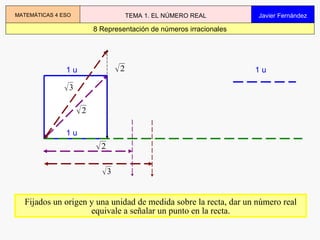
El documento describe los diferentes tipos de números reales, incluyendo números racionales (enteros y fraccionarios), irracionales, y la forma en que se pueden expresar y aproximar. Explica que los números racionales pueden expresarse como fracciones, mientras que los irracionales no, y deben aproximarse mediante decimales. También cubre conceptos como intervalos, el orden de los números reales, y las operaciones con números aproximados.

1. Los números racionales Un número fraccionario queda determinado y simbolizado por una fracción o cualquiera de sus fracciones equivalentes. Los números enteros y los fraccionarios forman el conjunto de los números racionales, que se designa por Q. 1. Los números racionales MATEMÁTICAS 4 ESO TEMA 1. EL NÚMERO REAL Javier Fernández Racionales Enteros Fraccionarios 27 9 3  4 9

2. Números que no se pueden expresar en forma fraccionaria 2b 2 = a 2 2. Números que no se pueden expresarn en forma racional MATEMÁTICAS 4 ESO TEMA 1. EL NÚMERO REAL Javier Fernández 2b 2 = 4k 2 2 divide a a a = 2k 2 divide a b Imposible b 2 =2k 2

3. La expresión decimal es periódica mixta: Todo número fraccionario puede expresarse en forma decimal sin más que efectuar la división entre el numerador y el denominador. Pueden entonces ocurrir los siguientes casos: La expresión decimal es exacta: La expresión decimal es periódica pura: Cuidado : algunas calculadoras redondean 3. Expresión decimal de los números fraccionarios MATEMÁTICAS 4 ESO TEMA 1. EL NÚMERO REAL Javier Fernández

4. El error absoluto de una expresión decimal es la diferencia entre ésta y el número representado, considerada positivamente. El error relativo es el cociente entre el error absoluto y el número. La cota de error es la diferencia entre las aproximaciones por exceso y por defecto con el mismo número de decimales. El error absoluto de la primera aproximación es 1,4142… – 1,4 = 0,0142 … 4. Aproximación, error y redondeo MATEMÁTICAS 4 ESO TEMA 1. EL NÚMERO REAL Javier Fernández Al elegir 1,4 como valor aproximado de se tiene una aproximación por defecto. Al elegir 1,5 como valor aproximado de se tiene una aproximación por exceso. La cota de error que se puede producir aproximando hasta las décimas es 0,1. El error relativo de la primera aproximación será 0,01.

5. q = 2‚4 78 78 78 78 ……. Un número decimal periódico: Pasos: Primero 1000q = 2478,787878…. Segundo 10q = 24,78787878.… Tercero 990q = 2478 - 24 Cuarto 5. Forma fraccionaria de un número decimal periódico MATEMÁTICAS 4 ESO TEMA 1. EL NÚMERO REAL Javier Fernández

6. Las expresiones decimales no periódicas se llaman números irracionales; estos números no se pueden expresar en forma de fracción. Los números racionales e irracionales forman el conjunto de los números reales, que se designa por R. 6. Los números reales. Ampliaciones de los conjuntos de los números MATEMÁTICAS 4 ESO TEMA 1. EL NÚMERO REAL Javier Fernández

7. Ejemplos El número  con 1000 cifras decimales 3 ,14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196442881097566593344612847564823378678316527120190914564856692346034861045432664821339360726024914127372458700660631558817488152092096282925409171536436789259036001133053054882046652138414695194151160943305727036575959195309218611738193261179310511854807446237996274956735188575272489122793818301194912983367336244065664308602139494639522473719070217986094370277053921717629317675238467481846766940513200056812714526356082778577134275778960917363717872146844090122495343014654958537105079227968925892354201995611212902196086403441815981362977477130996051870721134999999837297804995105973173281609631859502445945534690830264252230825334468503526193118817101000313783875288658753320838142061717766914730359825349042875546873115956286388235378759375195778185778053217122680661300192787661119590921642 ... Un número decimal cuya ley de formación es no periódica 2 ,020020002000020000020000002000000020000000020000000002…... 7. Algunos números irracionales MATEMÁTICAS 4 ESO TEMA 1. EL NÚMERO REAL Javier Fernández

8. 8 Representación de números irracionales MATEMÁTICAS 4 ESO TEMA 1. EL NÚMERO REAL Javier Fernández 1 u 1 u 1 u Fijados un origen y una unidad de medida sobre la recta, dar un número real equivale a señalar un punto en la recta.

9. La determinación de números reales se hace por aproximaciones sucesivas. 9. Determinación de números reales: Aproximaciones MATEMÁTICAS 4 ESO TEMA 1. EL NÚMERO REAL Javier Fernández

10. 10. Intervalos encajados MATEMÁTICAS 4 ESO TEMA 1. EL NÚMERO REAL Javier Fernández 1 2 1,9 2,0 1,91 1,92 1,912 1,913

11. Es imposible sumar exactamente dos números irracionales ya que tienen infinitas cifras decimales. Se opera con ellos sustituyéndolos por números aproximados con un número finito de cifras. 11. Suma aproximada de números reales MATEMÁTICAS 4 ESO TEMA 1. EL NÚMERO REAL Javier Fernández

12. Es imposible multiplicar exactamente dos números irracionales ya que tienen infinitas cifras decimales. Se opera con ellos sustituyéndolos por números aproximados con un número finito de cifras. 12 Producto aproximado de números reales MATEMÁTICAS 4 ESO TEMA 1. EL NÚMERO REAL Javier Fernández

13. La ordenación de números reales, <, menor que, se define así a < b  b – a es positivo Para comparar números reales se pasan previamente a forma decimal. Luego se comparan los números decimales. ¿Cuál es menor? Se deduce que o que Una interpretación 13. Orden en ℝ MATEMÁTICAS 4 ESO TEMA 1. EL NÚMERO REAL Javier Fernández

14. Los intervalos están determinados por dos números que se llaman extremos. En las figuras se indica por: circulito negro si el extremos se considera del intervalo. circulito blanco si el extremo no se considera del intervalo 14. Intervalos finitos MATEMÁTICAS 4 ESO TEMA 1. EL NÚMERO REAL Javier Fernández

15. Las semirrectas están determinadas por un número; en una semirrecta se encuentran todos los números mayores (o menores) que él. 15. Semirrectas MATEMÁTICAS 4 ESO TEMA 1. EL NÚMERO REAL Javier Fernández

16. Se define el valor absoluto de un número real x de la siguiente forma: Significado geométrico del valor absoluto de la diferencia de dos números Longitud del segmento AB =distancia entre los puntos A y B = |b – a| = |a – b| 16. Valor absoluto MATEMÁTICAS 4 ESO TEMA 1. EL NÚMERO REAL Javier Fernández O A a B b

17. Un intervalo de la forma (a – r, a + r) se llama entorno abierto de centro a y radio r. Un intervalo de la forma [a – r, a + r] se llama entorno cerrado de centro a y radio r. Para que x esté en el intervalo se ha de cumplir: |x – 4| < 2 Para que x esté en el intervalo se ha de cumplir: |x – 4|  2 17. Entorno de un punto MATEMÁTICAS 4 ESO TEMA 1. EL NÚMERO REAL Javier Fernández x x