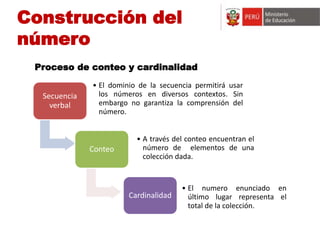
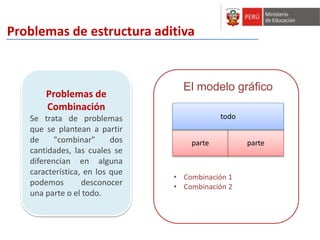
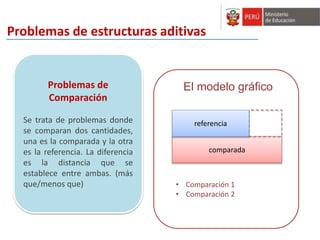
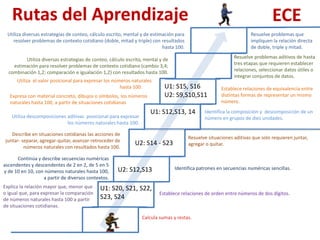
El taller busca fortalecer las capacidades de especialistas de soporte pedagógico en procesos didácticos para la construcción de nociones matemáticas. Se discuten estrategias para que los estudiantes comprendan la inclusión jerárquica, la decena, y formas de representar cantidades. Se proponen juegos didácticos para trabajar estas nociones usando material concreto.