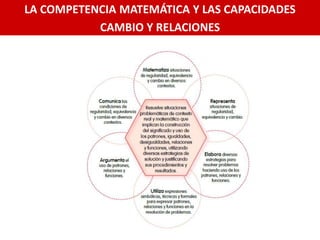
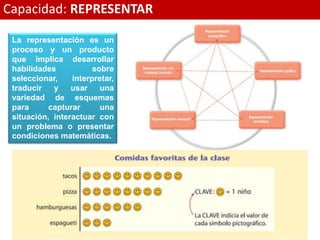
El documento presenta información sobre el enfoque de aprendizaje centrado en la resolución de problemas en matemáticas. Explica que este enfoque busca que los estudiantes valoren la matemática a través de resolver situaciones problemáticas cercanas a la vida real. También describe las competencias y capacidades matemáticas clave como números y operaciones, y cambio y relaciones. Finalmente, ofrece ejemplos de cómo conceptualizar e implementar este enfoque en el aula a través de casos y discusión en grupos.

1. ¿QUÉ Y CÓMO APRENDEN
NUESTROS NIÑOS Y NIÑAS?

2. ¿Qué
expectativas
tengo sobre
este taller?

3. OBJETIVOS DEL TALLER
o Identificar la relación que existe entre las rutas de aprendizaje y los
demás elementos del sistema curricular.
o Comprender el enfoque de matemática centrado en la resolución de
problemas y su perspectiva intercultural.
o Comprender las competencias, capacidades e indicadores
planteados en los fascículos de matemática en el marco de un
currículo por competencias.
o Vivenciar e identificar situaciones reales de aprendizaje en
matemática acordes al enfoque de la matemática.

4. SISTEMA CURRICULAR
Punto de
partida y
punto de
llegada

5. APRENDIZAJES
FUNDAMENTALES
el derecho de todos los
estudiantes
PEN Objetivo 2
El punto de partida:
situación curricular actual
El punto de llegada:
los aprendizajes fundamentales como
derecho en el marco de un sistema
articulador y orientador

6. El punto de partida:
Brecha entre el currículo prescrito y el
implementado
Explicitar las
intenciones y
demandas
educativas de una
sociedad
Orientar la labor
docente
Implica lo que
efectivamente se
pone en práctica
para los
estudiantes en las
escuelas

7. CARACTERÍSTICAS:
Baja densidad
Gradualidad
Pertinencia
CONDICIONES QUE DEBE
CUMPLIR EL CURRÍCULO
PRESCRITO

8. El punto de partida:
situación curricular que
encuentra el docente
2363 conocimientos
2158 capacidades
1114 actitudes
151 competencias
Un Diseño curricular
nacional
DCR 1:
Inicial: 379 conocimientos y
capacidades, 143 actitudes.
Primaria: 806 capacidades, 413
actitudes, 989 conocimientos.
Secundaria: 1466 capacidades,
113 actitudes y 2017
conocimientos
DCR 2:
Inicial: 680 capacidades, 400
actitudes.
Primaria y Secundaria: 2464
capacidades, 312 actitudes y 921
conocimientos
Varios GR (6) con
Diseños curriculares
propios
Comunicación
Matemática
…
se organizan en
dominios, niveles con
sus respectivos
indicadores
Mapas de progreso

9. Punto de
llegada
Es necesario que:
Se hace necesario identificar y definir LOS
APRENDIZAJES FUNDAMENTALES que
TODOS TIENEN DERECHO A LOGRAR
 Claros y orientadores de la práctica
docente
 Que concrete las intenciones educativas
en términos de competencias.
 Que permita “alinear” currículo y
estándares y presentarlos en progresión.
Práctica docente
Mapas
de
progreso
DCN
DCR

10. Nuestro punto de
llegada

11. Cada uno de los instrumentos curriculares debe
abordar el aprendizaje a partir de diferentes
funciones.

12. Presentan un menor número de
competencias y capacidades los cuales
han sido elaborados a partir del DCN y
los mapas de progreso.
Se organiza por competencias,
capacidades e indicadores.
Las competencias y capacidades son
las mismas para toda la EBR. Los
indicadores dan cuenta de los logros y
progresos de las capacidades y son los
que cambian.
Rutas del
aprendizaje

13. Competencias en el
DCN
Comprende críticamente diversos
tipos de textos escritos en variadas
situaciones comunicativas según su
propósito de lectura mediante
procesos de interpretación y reflexión.
Competencia de
comprensión de textos
en las rutas del
aprendizaje

14. Documentos e instrumentos
que componen la ruta de los
aprendizajes
Fascículos generales por cada
aprendizaje fundamental
Fascículos por cada ciclo y
ámbito de aprendizaje
Fascículos para la gestión de
los aprendizajes
Kit para evaluar los
aprendizajes
Rutas de
aprendizaje

15. Escenario
2013 Conviven de manera paralela el DCN, Mapas
de progreso y rutas de aprendizaje.
Las rutas definen con claridad las
competencias, capacidades a lograr en
comunicación, en matemática y en ciudadanía.
Se pondrá en consulta los aprendizajes
fundamentales.
Al término del 2013 se aprobará el Marco
Curricular que definirá los aprendizajes
fundamentales.
Se irán alineando los diferentes instrumentos
que componen el sistema curricular: marco
curricular, mapas de progreso, rutas de
aprendizaje y los currículos regionales.

16. MATEMÁTICA

17. COMPRENDIENDO EL
ENFOQUE DE LA
MATEMATICA

18. ¿Qué conoces sobre el enfoque
de la matemática?

31. ¿Qué papel cumple la
matemática en la vida?
¿Crees que la escuela responde
a estos requerimientos?
¿Cómo estamos enseñando?

32. Leamos nuestros fascículos de Matemática
¿Qué reflexión les deja los
casos planteados?
¿Qué semejanzas y
diferencias encuentras con
las prácticas cotidianas
que se dan en las aulas
actualmente?
fascículo III Pág. 7 al 8 y
fascículo IV y V Pág. 9 al 11

33. Trabajo en equipos
Resolvamos situaciones problemáticas y
reflexionemos.

34. 1 2
4 3
RELEVANCIA SOCIAL ALTA
RELEVANCIA SOCIAL BAJA
Algoritmos
Ejercicios
Datos descontextualizados
Datos inventados
Lejos de la realidad.
Adquiere relevancia porque
parte de la realidad.
Adquiere significado.
A veces carece de utilidad social.
Aprendizaje in situ.
Simulaciones situadas.

35. Surge la necesidad de plantear y ASUMIR
un modelo formativo. Un enfoque:
Aprendizaje Centrado en la
Resolución de Problemas.

36. El conocimiento matemático fue construido a partir
de la necesidad de resolver problemas.
El conocimiento
matemático fue
construido a
partir de la
necesidad de
resolver
problemas.

37. El enfoque problémico
consiste en promover formas
de enseñanza-aprendizaje
que den respuesta a
situaciones problemáticas
cercanos a la vida real.
Es el medio principal
para establecer
relaciones de
funcionalidad
matemática con la
realidad cotidiana.

38. ¿Qué caracteriza al enfoque problémico o
centrado en la resolución de problemas?
La resolución de situaciones problemáticas ha
dado pie a la construcción del conocimiento.
Busca que los estudiantes valoren y
aprecien el conocimiento matemático.
Relaciona la resolución de situaciones
problemáticas con el desarrollo de
capacidades matemáticas.
La matemática, trasciende la escuela y se
manifiesta en el desarrollo socio cultural de los
pueblos.

39. LOS INICIOS DEL ESTUDIO DE LA
GEOMETRIA SE HAN DADO A PARTIR DE
DAR SOLUCIÓN A LOS PROBLEMAS QUE
REQUERIAN CREAR UN SISTEMA DE
MEDICIÓN Y CÁLCULO DE ÁREAS QUE
PERMITIERA DELIMITAR LAS PARCELAS
CON EXACTITUD.
REGISTRAR LA CANTIDAD DE MUERTES POR LA
PESTE BUBONICA POR MAS DE 50 AÑOS
PERMITIO UN ESTUDIO MUNISIOSO DANDO
INICIO A ESTUDIO DE ANALISID DE DATOS.
La resolución de situaciones problemáticas ha dado pie al la
construcción del conocimiento.

40. La resolución de problemas moviliza el saber actuar en los
estudiantes lo que permite que cada uno de ellos, se sienta
capaz de resolver situaciones problemáticas y de aprender
matemáticas, considerándola útil y con sentido para la vida.
Busca que los estudiantes valoren y aprecien el conocimiento
matemático.

41. Relaciona la resolución de situaciones problemáticas con el
desarrollo de capacidades matemáticas.

42. La matemática, trasciende la escuela y se manifiesta en el
desarrollo socio cultural de los pueblos.
El enfoque de resolución de problemas oficializa y legitima a la
etnomatemáticas o matemáticas de los pueblos originarios.

43. VALORACIÓN DE LA EDUCACIÓN MATEMÁTICA
FUNCIONAL
INSTRUMENTAL
FORMATIVO
Promueve el desarrollo de formas
de pensar, construir conceptos y
resolver situaciones problemáticas.
Utilidad para dar respuestas a
necesidades socioculturales,
científicas y personales.
Provee de herramientas simbólicas y
procedimientos útiles en la
resolución de problemas.
En resumen la Matemática…

44. Trabajo en equipos
En equipos utilicen un organizador visual
que sintetice las ideas principales del
enfoque de Resolución de Problemas.

45. COMPETENCIAS
CAPACIDADES E
INDICADORES

46. UNA COMPETENCIA MATEMÁTICA ES…
La competencia
matemática es un
saber actuar en un
contexto particular,
que nos permite
resolver
situaciones
problemáticas
reales o de
contexto
matemático.

47. LA
COMPETENCIAS
EN
MATEMATICA

49. LA COMPETENCIA MATEMÁTICA Y LAS CAPACIDADES
NÚMERO Y OPERACIONES

50. LA COMPETENCIA MATEMÁTICA Y LAS CAPACIDADES
CAMBIO Y RELACIONES

51. Números y operaciones
Matematiza situaciones que involucran
cantidades y magnitudes en diversos
contextos.
Representa situaciones que involucran
cantidades y magnitudes en diversos
contextos.
Comunica situaciones que involucran
cantidades y magnitudes en diversos
contextos.
Elabora estrategias haciendo uso de los
números y sus operaciones para resolver
problemas.
Utiliza expresiones simbólicas y formales de
los números y las operaciones en la resolución
de problemas.
Argumenta el uso de los números y sus
operaciones en la resolución de problemas.
Cambio y relaciones
Matematiza situaciones de regularidad,
equivalencia y cambio en diversos contextos.
Representa situaciones de regularidad,
equivalencia y cambio en diversos contextos.
Comunica las condiciones de regularidad,
equivalencia y cambio en diversos contextos.
Elabora estrategias haciendo uso de los
patrones, relaciones y funciones para resolver
problemas.
Utiliza expresiones simbólicas y formales de
los patrones, relaciones y funciones en la
resolución de problemas.
Argumenta el uso de los patrones, relaciones y
funciones para resolver problemas.
CAPACIDADES MATEMÁTICAS

52. Matematizar implica, expresar la realidad, un contexto concreto o una situación en el
mundo real, en términos matemáticos.
Capacidad: MATEMATIZAR

53. La representación es un
proceso y un producto
que implica desarrollar
habilidades sobre
seleccionar, interpretar,
traducir y usar una
variedad de esquemas
para capturar una
situación, interactuar con
un problema o presentar
condiciones matemáticas.
Capacidad: REPRESENTAR

54. la capacidad de la comunicación matemática implica promover el
diálogo, la discusión, la conciliación y/o rectificación de ideas.
Esto permite al estudiante familiarizarse con el uso de
significados matemáticos e incluso con un vocabulario
especializado.
Capacidad: COMUNICAR

55. Capacidad: ELABORAR ESTRATEGIAS
Esta capacidad consiste en seleccionar o elaborar un plan o estrategia
sobre cómo utilizar la matemática para resolver problemas de la vida
cotidiana,… (Fascículo 1 III ciclo, pág. 49)

56. Capacidad: UTILIZA EXPRESIONES SIMBÓLICAS, TÉCNICAS Y
FORMALES
El uso de expresiones y
símbolos matemáticos
ayudan a la formalización
de las nociones
matemáticas. Estas
expresiones no son fáciles
de asimilar debido a la
complejidad de los
procesos que implica la
simbolización. (Fascículo 1 III
ciclo, pág. 51)

57. Así, se dice que la argumentación puede tener tres diferentes usos:
 Explicar procesos de resolución de situaciones problemáticas
 Justificar, es decir, hacer una exposición de las conclusiones o resultados a
los que se haya llegado
 Verificar conjeturas, tomando como base elementos del pensamiento
matemático.
Capacidad: ARGUMENTA

58. INDICADORES
Los indicadores son enunciados que describen
comportamientos de una capacidad.

59. INDICADORES

60. Trabajo en equipos
En equipos vivenciemos situaciones
matemáticas e identifiquemos las
capacidades movilizadas.

61. En la situación problemática que haz vivenciado
identifica como se ha movilizado las capacidades
matemáticas:
CAPACIDADES ¿CÓMO SE HA MOVILIZADO?
Matematizar
Representar
Comunicar
Elaborar diversas
estrategias
Utilizar expresiones
Simbólicas
Argumentar

62. Trabajo en equipos
En equipos establezcan la gradualidad en
los indicadores.

63. INTERRELACIÓN Y GRADUALIDAD DE
LOS INDICADORES EN EL CARTEL
Utiliza
estrategias de
conteo (conteo
de uno en uno
y agrupando)
para resolver
problemas de
contexto
cotidiano que
implican
acciones de
agregar, quitar
y juntar con
resultados
hasta cinco
objetos.
Utiliza diversas
estrategias de
conteo, cálculo
escrito, mental
y de
estimación
para resolver
problemas de
contexto
cotidiano
(cambio 1,2;
combinación 1
y doble) con
resultados
hasta 20.
Utiliza diversas
estrategias de
conteo, cálculo
escrito, mental y
de estimación
para resolver
problemas de
contexto
cotidiano
(cambio 3, 4;
combinación 1
y2;
comparación e
igualación 1y2;
doble, mitad y
triple) con
resultados
hasta 100.
Usa diversas
estrategias de
cálculo escrito
y mental para
resolver
problemas
aditivos,
multiplicativos
y de
combinación
de las cuatro
operaciones
con números
naturales
hasta cuatro
cifras.
Usa diversas
estrategias
de cálculo
escrito y
mental, para
resolver
situaciones
problemática
s aditivas y
multiplicativa
s, de doble
mitad, triple,
cuádruple
con números
naturales de
hasta tres
cifras.
Usa estrategias
que implican el uso
de la
representación
concreta y gráfica
(dibujos, cuadros,
esquemas,
gráficos, etc.), para
resolver
situaciones
problemáticas de
igualación y
comparación 5 y 6
y situaciones
multiplicativas de
combinación-
división (producto
cartesiano) y
comparación.
Usa diversas
estrategias que
implican el uso
de la
presentación
concreta y gráfica
(dibujos, cuadros,
esquemas,
gráficos, etc.),
para resolver
situaciones
problemáticas
aditivas y
multiplicativas,
usando números
naturales hasta
seis cifras.

64. ¡¡MUCHAS GRACIAS!!