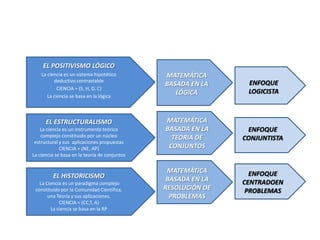
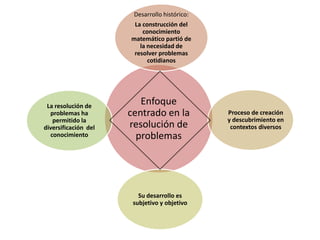
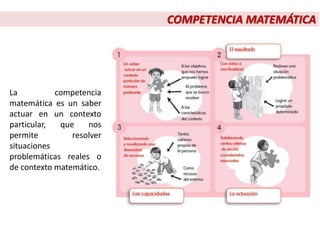
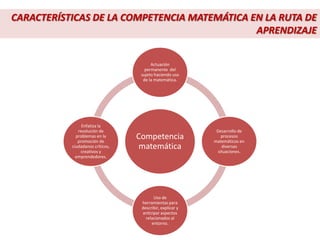
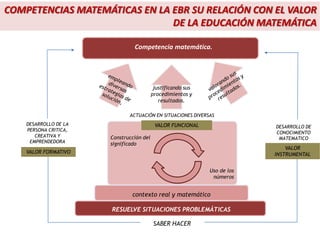
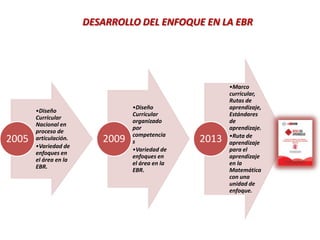
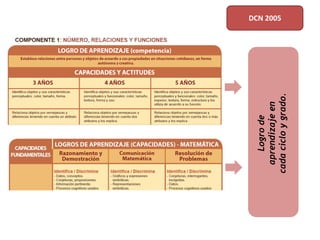
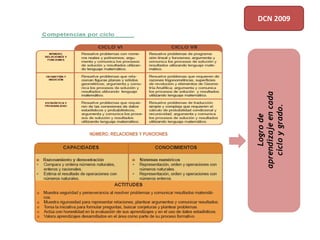
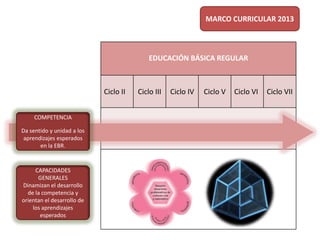
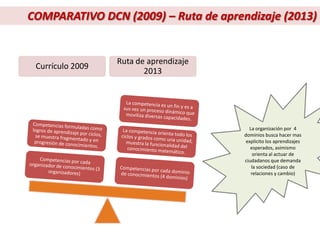
Este documento describe el enfoque centrado en la resolución de problemas para la enseñanza de las matemáticas. Explica que este enfoque se basa en que la resolución de situaciones problemáticas es la actividad central de las matemáticas y que permite establecer relaciones funcionales con la realidad cotidiana. Además, busca que los estudiantes valoren el conocimiento matemático. Finalmente, señala que la resolución de problemas debe impregnar todo el currículo de matemáticas y servir como contexto para desarrollar