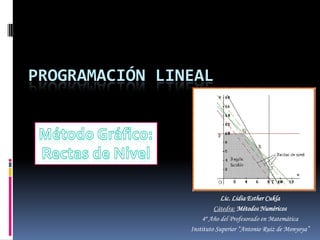
El documento explica el método gráfico de programación lineal mediante rectas de nivel que representan valores constantes de una función objetivo. Se utiliza un ejemplo de un fabricante que quiere maximizar su ganancia produciendo jeans azules y negros, sujeto a restricciones de producción. La solución óptima se encuentra en el punto donde la recta de nivel máximo toca la región factible, en este caso, produciendo 700 jeans azules y 100 jeans negros para una ganancia máxima de $12000.

1. Programación LinealMétodo Gráfico:Rectas de NivelLic. Lidia Esther CuklaCátedra:Métodos Numéricos 4º Año del Profesorado en MatemáticaInstituto Superior “Antonio Ruiz de Monyoya”

2. Método de las Rectas de NivelLas rectas de nivel dan los puntos del plano en los que la función objetivo toma el mismo valor.Si la función objetivo es f(x,y) = ax + by + c, la ecuación de las rectas de nivel es de la forma:ax + by + c = 0 ax+ by = kVariando kse obtienen distintos niveles para esas rectas y, en consecuencia, distintos valores para f(x,y).En un problema todas las rectas de nivel son paralelas, pues los coeficientes a y b de la recta ax + by = k son los que determinan su pendiente. Por tanto, si k1 es distinto de k2 , las rectas ax + by = k1y ax + by = k2son paralelas. Luego, trazada una cualquiera de esas rectas, las demás de obtienen por desplazamientos paralelos a ella.Si lo que se pretende es resolver un problema de programación lineal, los únicos puntos que interesan son los de la región factible, y las únicas rectas de nivel que importan son aquellas que están en contacto con dicha región. Como el nivel aumenta (o disminuye) desplazando las rectas, el máximo (o el mínimo) de f(x,y) se alcanzará en el último (o en el primer) punto de contacto de esas rectas con la región factible.

3. Veamos ahora como se aplica todo esto a la resolución de un problema de programación lineal :Por ejemplo:Para satisfacer las demandas de sus distribuidores, un fabricante debe producir por día no menos de 400 y no más de 800 jeans azules, y no menos de 100 y no más de 300 jeans negros. Además, para mantener una buena calidad, no debe producir en total más de 800 jeans por día. Sabiendo que obtiene una ganancia de $16 por cada jeans azul y de $8 por cada jeans negro, desea saber cuál debe ser la producción diaria de cada tipo de jeans para maximizar la ganancia.La cantidad que deseamos maximizar (la ganancia) puede expresarse en forma de una función lineal, llamando x a la cantidad de jeans azules e y a la cantidad de jeans negros, tenemos: f(x,y) = 16x + 8y Por otra parte, las restricciones impuestas por las condiciones dadas se puede expresar en forma de inecuaciones lineales: 400  x  800100  y  300x + y 800

4. Es decir, se trata de maximizar la función f(x,y) = 16x + 8y Sujeta a Para hallar el conjunto S de soluciones factibles debemos representar gráficamente el sistema de inecuaciones planteado. Los puntos que pertenecer a la región S - región factible - son las posibles soluciones del problema.Los vértices se hallan resolviendo las ecuaciones simultáneas apropiadas. Por ejemplo, el vértice (500,300) se obtiene resolviendo el sistema SS

5. Luego representamos las rectas de nivel : En este caso son rectas de la forma 16x + 8y = k Inicialmente representamos 16x + 8y = 0

6. Luego representamos las rectas de nivel : En este caso son rectas de la forma 16x + 8y = k Inicialmente representamos 16x + 8y = 0 Trasladándola hacia la derecha, obtenemos, por ejemplo 16x + 8y = 1600

7. Luego representamos las rectas de nivel : En este caso son rectas de la forma 16x + 8y = k Inicialmente representamos 16x + 8y = 0 Trasladándola hacia la derecha, obtenemos, por ejemplo16x + 8y = 160016x + 8y = 4800

8. Luego representamos las rectas de nivel : En este caso son rectas de la forma 16x + 8y = k Inicialmente representamos 16x + 8y = 0 Trasladándola hacia la derecha, obtenemos, por ejemplo16x + 8y = 160016x + 8y = 480016x + 8y = 8000

9. Luego representamos las rectas de nivel : En este caso son rectas de la forma 16x + 8y = k Inicialmente representamos 16x + 8y = 0 Trasladándola hacia la derecha, obtenemos, por ejemplo16x + 8y = 160016x + 8y = 480016x + 8y = 800016x + 8y = 12000

10. Luego representamos las rectas de nivel : En este caso son rectas de la forma 16x + 8y = k Inicialmente representamos 16x + 8y = 0 Trasladándola hacia la derecha, obtenemos, por ejemplo16x + 8y = 160016x + 8y = 480016x + 8y = 800016x + 8y = 12000Solución óptimaDe esta manera se obtiene en el punto de la región factible que hace máximo k. En nuestro caso esto ocurre en el punto (700, 100); es el último punto de contacto de esas rectas con la región factible , para el que k = 12000.Es decir, el fabricante debe producir 700 jeans azules y 100 jeans negros para obtener su ganancia diaria máxima, que en este caso es de $12000.