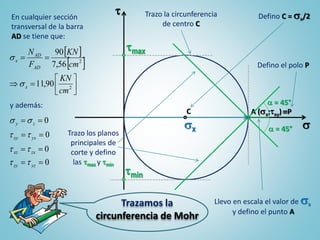
El documento presenta la resolución de un problema de resistencia de materiales sobre un reticulado plano. Se solicita dimensionar la barra AD mediante el cálculo de esfuerzos. Luego, determinar los planos principales de corte y tensiones de una sección transversal de la barra dimensionada usando la circunferencia de Mohr. El autor dimensiona la barra AD como un perfil doble L 50 x 30 x 5 que cumple con las tensiones admitidas. Finalmente, traza la circunferencia de Mohr para definir los planos principales de corte y las máxim

1. Solicitación Axil
Resolución del Problema N° 16
Curso de Estabilidad IIb
Ing. Gabriel Pujol
Para las carreas de Ingeniería Mecánica e Ingeniería Naval y Mecánica de la
Facultad de Ingeniería de la Universidad de Buenos Aires

2. Resolvamos el
siguiente
reticulado
Enunciado
Dado el reticulado plano que se indica en la figura, cuyas barras serán construidos por
dos perfiles ángulo de alas desiguales (según norma DIN 1029) se solicita:
• Dimensionar la barra AD.
Datos: a = 2m; P1 = P2 = P3 = 30 KN; adm = 12 KN/cm2
• Determinar para la barra dimensionada los planos principales de corte y sus
respectivas tensiones mediante la circunferencia de Mohr.

3. Dimensionemos la
barra AD
Resolución
Las reacciones de vínculo en los apoyos A y B actúan hacia
arriba, y por razones de simetría (geométrica y de cargas),
tienen la misma magnitud:
 KNPRR
i
iBA 45
2
1 3
1
 
Para calcular el esfuerzo en la barra, se
realiza el diagrama del cuerpo libre en el
nudo A, como se muestra en la figura:
  '34265,0
2
1
tan  en donde será:

4. Planteando las dos ecuaciones de equilibrio
de proyección de fuerzas tendremos:
Sobre el eje “y”:
   KN
KNR
N
NRP
A
AC
ACAiy
63,100
)'3426sin(
45
)sin(
)sin(0






(compresión)
Sobre el eje “x”:
    KNKNNN
NNP
ACAD
ACADix
90)'3426cos(.63,100)cos(
)cos(0




(tracción)

5. Para dimensionar la barra (AD) debe
cumplirse que:
   2
2
5,7
12
90
cm
cm
KN
KN
F 





adm
ADAD
adm
N
F
F
N

 
De la tabla de perfiles
(L - DIN 1029) se obtiene:
como la barra está conformada
por dos perfiles idénticos será:
 
 2
2
75,3
2
5,7
2
cmF
cmF
F
Perfil
Perfil


Perfil seleccionado: L 50 x 30 x 5

6. Trazamos la
circunferencia de Mohr
En cualquier sección
transversal de la barra
AD se tiene que:
 
 








2
2
90,11
56,7
90
cm
KN
cm
KN
F
N
x
AD
AD
x



t
x
y además:
0
0
0
0




yzzy
zxxz
yxxy
zy
tt
tt
tt

A (x;txy)C
Defino C = x/2Trazo la circunferencia
de centro C
Llevo en escala el valor de x
y defino el punto A
P
Defino el polo P
Trazo los planos
principales de
corte y defino
las tmax y tmin
tmax
tmin
 = 45°
 = 45°

7. Bibliografía
Estabilidad II - E. Fliess
Introducción a la estática y resistencia de materiales - C. Raffo
Mecánica de materiales - F. Beer y otros
Resistencia de materiales - R. Abril / C. Benítez
Resistencia de materiales - Luis Delgado Lallemad / José M. Quintana Santana
Resistencia de materiales - V. Feodosiev
Resistencia de materiales - A. Pytel / F. Singer
Resistencia de materiales - S. Timoshenko

8. Muchas Gracias