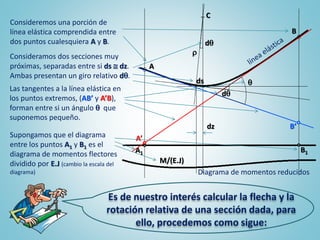
Este documento resume los conceptos fundamentales de la flexión de vigas, incluyendo la curvatura de la fibra neutra bajo cargas, el alargamiento de las fibras, el cálculo del radio de curvatura, el diagrama de momentos reducidos, y los teoremas para calcular la rotación y flecha de una sección dada de una viga basándose en el área bajo la curva del diagrama de momentos.

1. Deformaciones en la
Flexión
Diagrama de Momentos Reducidos
Curso de Estabilidad IIb
Ing. Gabriel Pujol
Para las carreas de Ingeniería Mecánica e Ingeniería Naval y Mecánica de la
Facultad de Ingeniería de la Universidad de Buenos Aires

2. Consideremos una viga sometida a flexión,
empotrada en un extremo y libre en el otro:
Introducción
Bajo la acción de las cargas, la fibra neutra adopta
una determinada curvatura
La fibra más alejada experimenta un alargamiento
total: d1
de los triángulos semejantes OCE y OC’E’ se deduce
que:




 v
d
dv
EC
CE





1
1
''
Conforme a la Ley de Hooke:


v
EE max
que debe igualar a: (tensión normal en flexión)v
J
M
max
de donde:
JE
M



1

3. Tomando sobre la elástica dos puntos a y b.
Las normales trazadas por estos puntos se
cortan en C, verificándose:
y por ser  un ángulo pequeño será:
Introducción
JE
M
ds
d
dds





1














1
1
2
2
dz
dy
dz
d
dz
dy
tg
y
dz
d
dzds
JE
M
dz
yd
JE
M
dz
yd
dz
d



 2
2
2
2
1


Radio de Curvatura
como para valores crecientes de z corresponden
valores decrecientes de  habrá que afectar la
expresión anterior con un signo menos (-), así:

4. Es de nuestro interés calcular la flecha y la
rotación relativa de una sección dada, para
ello, procedemos como sigue:
Consideremos una porción de
línea elástica comprendida entre
dos puntos cualesquiera A y B.
C
A
B
A1 B1

Supongamos que el diagrama
entre los puntos A1 y B1 es el
diagrama de momentos flectores
dividido por E.J (cambio la escala del
diagrama)
M/(E.J)
Las tangentes a la línea elástica en
los puntos extremos, (AB’ y A’B),
forman entre si un ángulo  que
suponemos pequeño.
A’
B’
Consideramos dos secciones muy
próximas, separadas entre si ds  dz.
Ambas presentan un giro relativo d.
dz
ds 
d
d
Diagrama de momentos reducidos

5. La rotación relativa de una sección dada, la
calculamos como sigue:
C
A
B
A1 B1

M/(E.J)
A’
B’dz
ds 
d
d
El área sombrada será:
 




B
A
dz
JE
M
JE
M
dz
d
ds
d


El resultado de la integral dada por
esta ecuación no es sino el área del
diagrama de momentos reducidos.
TEOREMA I: “El ángulo  comprendido
entre dos tangentes en dos puntos
cualesquiera A y B de la línea elástica,
es igual al área total del trozo
correspondiente del diagrama de
momentos reducidos.”

6. La flecha de una sección dada, la calculamos
como sigue. Observemos el segmento BB’:
C
A
B
A1 B1

M/(E.J)
A’
B’dz
ds 
d
d
dfdz  
Podemos apreciar que cada segmento
ds de la elástica contribuye a la longitud
f en una cantidad:
f
df
z
integrando estas distancias podemos
obtener el valor de f:
 


B
A
B
A
dzz
JE
M
dzf 
Momento estático con respecto a B del
área del diagrama de momentos reducidos
TEOREMA II: “Dado dos puntos A y B
pertenecientes a una línea elástica,
la ordenada de B respecto a la
tangente en A es igual al momento
estático con respecto a B del área de
momentos reducidos comprendida
entre A y B.”

7. Bibliografía
Estabilidad II - E. Fliess
Introducción a la estática y resistencia de materiales - C. Raffo
Mecánica de materiales - F. Beer y otros
Resistencia de materiales - R. Abril / C. Benítez
Resistencia de materiales - Luis Delgado Lallemad / José M. Quintana Santana
Resistencia de materiales - V. Feodosiev
Resistencia de materiales - A. Pytel / F. Singer
Resistencia de materiales - S. Timoshenko

8. Muchas Gracias