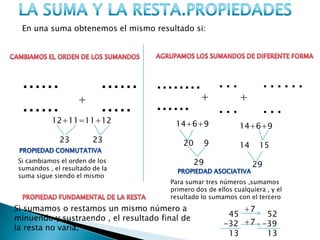
Este documento describe las propiedades y operaciones básicas con números naturales, incluyendo la suma, resta, multiplicación y expresiones combinadas. Explica las propiedades conmutativa, asociativa y distributiva, así como el uso de paréntesis y la jerarquía de operaciones. También incluye ejemplos prácticos de cómo aplicar estas propiedades y realizar cálculos con números naturales.

1. OPERACIONES CON
NÚMEROS NATURALES

2. ESQUEMA
LA SUMA Y LA RESTA PROPIEDADES
LA PROPIEDAD DISTRIBUTIVA DE LA MULTIPLICACIÓN
EXPRESIONES CON OPERACIONESCOMBINADAS

3. CONMUTATIVA
LA SUMA
PROPIEDADES
ASOCIATIVA
LA RESTA
PROPIEDAD
FUNDAMENTAL DE
LA RESTA
CONMUTATIVA
OPERACIONES CON
NÚMEROS
NATURALES
PROPIEDADES
ASOCIATIVA
PRÁCTICA DE LA
MULTIPLICACIÓN
DISTRIVUTIVA
LA
MULTIPLICACIÓN
USO DE
PARÉNTESIS
JERARQUÍA DE LAS
OPERACIONES
PRIORIDAD DE LA
MULTIPLICACIÓN

4. En una suma obtenemos el mismo resultado si:
......
......
+
...... ........ … ……
+
+
..... ...... … …
12+11=11+12
23
23
Si cambiamos el orden de los
sumandos , el resultado de la
suma sigue siendo el mismo
14+6+9
20
9
29
14+6+9
14
15
29
Para sumar tres números ,sumamos
primero dos de ellos cualquiera , y el
resultado lo sumamos con el tercero
Si sumamos o restamos un mismo número a
minuendo y sustraendo , el resultado final de
la resta no varía.
+7
45
52
-32 +7 -39
13
13

5. En sumas o restas
combinadas , el paréntesis
nos indica la operación
que tenemos que hacer en
primer lugar
859 - (437+286) =
= 859 – 723 = 136

6. ..... ..
..... ..
..... ..
5
.... ..
.... ..
.... ..
2
3
2
(5+2)x3=7x3=21abejas
(5x3)+(2x3)=15+6=21abejas
El producto de una suma por un
número es igual a la suma de los
productos de cada uno de los
sumandos por ese número
3
6
(6-2)x3=4x3=12
6x3-2x3=18-6=12
El producto de una diferencia
por un número es igual a la
diferencia de los productos de
cada termino por ese número

7. La multiplicación cumple también las propiedades conmutativa y asociativa.
5x4=4x5
(4x12)x2=48x2=96
4x(12x2)=4x24=96
Copia y calcula aplicando la propiedad asociativa
4x5x3
( x )x =
x( x )=

8. Observa cómo realizamos dos expresiones que tienen los mismos términos
pero diferentes resultados.
Primero , la multiplicación ;
después la resta.
Compro 4 tarros y
me descuentan 2€
10€
....
4x10-2=40-2=38
Primero , el paréntesis ;
después , la multiplicación.
Compro 4 tarros y
me rebajan 2€ en
cada uno
....
4x(10-2)=4x8=32
Para calcular expresiones combinadas , primero se realiza la operación
que está entre paréntesis ; después las multiplicaciones , y , por último
las sumas y las restas.
15-4x(8-5)=15-4x3=15-12=3

9. 7+(2+4)x3
7+6x3
7+18
25

10. Para calcular (8+3)x2 con la calculadora , escribimos:
8+3x2=22
Para calcular 8+3x2 , escribimos
8M+3x2M-MR=14
o bien
3x2+8=14

11. Para multiplicar 524 x 236 procedemos de la forma siguiente:
CM
DM
UM
C
D
U
5
2
4
x
2
3
6
3
1
4
4
1
5
7
2
0
1
0
4
8
0
0
1
2
3
6
6
4
524x6
524x30
524x200
En la práctica , no escribimos
los ceros finales de los
productos parciales y
situamos cada orden de
unidades en su columna
524
x236
3144
1572
+1048
123664

12. Los ceros finales de los factores no se
multiplican , se añaden al producto:
327x10=3270
327x20=6540
230x100=23000

13. Cuando hay ceros intermedios en
una multiplicación , dejamos el
espacio y seguimos multiplicando
346
x203
1038
+692
70238

14. http://www.ceipjuanherreraalcausa.es/Recursosdidacticos/QUINTO/datos/03_
Mates/datos/05_rdi/ud02/unidad02.htm
http://www.youtube.com/watch?v=xCuM2tDWCwo