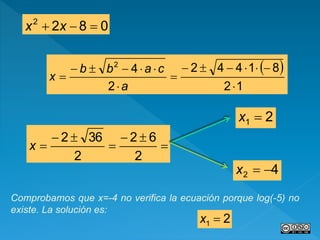
El documento explica el concepto de logaritmos, centrándose en su definición, propiedades y ejemplos prácticos de cálculo utilizando diferentes bases. Se abordan ejercicios para calcular logaritmos y resolver ecuaciones logarítmicas, así como la aplicación de propiedades matemáticas relacionadas. Además, se incluyen métodos para aproximar logaritmos y resolver sistemas de ecuaciones utilizando logaritmos.

1. XPLoga 
Profesor: Juan Sanmartín
Matemáticas
Recursos subvencionados por el…

2. Se llama logaritmo en base a de P, y se escribe loga P, al
exponente al que hay que elevar la base a para obtener P.
PaxPLog x
a 
Ejemplo:
8238log 3
2 
Leemos, logaritmo en base 2 de 8 es 3 porque 2 elevado a 3 es 8.

3. Análogamente podemos decir:
84,5310731105051,184,53log
0001,0
10000
1
10
1
1040001,0log
10000001061000000log
813481log
12553125log
731105051,1
10
4
4
10
6
10
4
3
3
5







4. Los logaritmos en base 10 se llaman
logaritmos decimales y son los más
utilizados. Por eso, la tecla de la
calculadora es para el cálculo de los
logaritmos decimales. (también en el
uso habitual podemos poner log en
lugar de log10 ).
Para Calcular, por ejemplo, log10
53,84 se hace:
53,84 1,731105051
El cálculo de logaritmos en otra base
se hace a partir de los logaritmos
decimales, como se verá en las
propiedades

5. Ejercicio 1.- Decir el valor de los logaritmos poniendo los números
en forma de potencias:
a. Log6 1296
b. Log2 0,125
41296log61296) 6
4
a
Ejercicio 2.- Con la tecla ,calcular log 5, log 50, log 500, log
5000
...69897,35000log
...69897,2500log
...69897,150log
...69897,05log




3125,0log2
2
1
8
1
1000
125
125,0) 2
3
3
 
b

6. Ejercicio 3.-Utilizando la tecla para hallar potencias, ^ ó xy ,
calcular de forma aproximada log7532.
,...3532log
24017
3437
74
3






...2,3532log
,...6147
,...5067
73,3
2,3






...22,3532log
...5367
...5267
,...5167
7
23,3
22,3
21,3









Así sucesivamente, podemos aproximarnos tanto como queramos
al valor de log7532.
Hallemos la cifra de las décimas
Hallemos la cifra de las centésimas

8. I.- El logaritmo de 1 es 0 cualquiera que sea la base.
01log a Ejemplo: 1501log 0
5 
II.- Cualquiera que sea la base, su logaritmo es 1.
1log aa 7717log 1
7 Ejemplo:
III.- El logaritmo de un producto es igual a la suma de los
logaritmos de los factores.
  QPQP aaa logloglog 
Ejemplo:
9368log64log)864(log512log 2222 
51229512log 9
2 

9. IV.- El logaritmo del cociente de dos números es igual al
logaritmo del dividendo menos el logaritmo del divisor.
QP
Q
P
aaa logloglog 
Ejemplo:
23527log243log
27
243
log 333 
9329log
27
243
log 2
33 
V.- El logaritmo de una potencia es igual al exponente por
el logaritmo de la base.
PnP a
n
a loglog 
Ejemplo:
236
49log349log 7
3
7



10. VI.- El logaritmo de una raíz es igual al logaritmo del
radicando dividido por el índice de la raíz.
n
P
P an
a
log
log  Ejemplo:
3
2
3
4log
4log 23
2 
Esta propiedad es consecuencia de la anterior debido a:
n
P
P
n
PP a
a
n
a
n
a
log
log
1
loglog
1

VII.- Cambio de base. El logaritmo en base a de un número
se puede obtener, a partir de los logaritmos decimales,
según la siguiente igualdad.
a
P
a
P
Pa
log
log
log
log
log
10
10
 De esta forma se puede hacer
por calculadora

11. Ejercicio 4.-Sabiendo que el log 2=0,301 y aplicando las
propiedades anteriores, calcula log 507.
50log750log 7

Ejercicio 5.-Con ayuda de la calculadora, obtener:
a. log2 1500
b. log7 593
Tecla
1500255074679,10
301029995,0
176091259,3
2log
1500log
1500log) 55074697,10
2 a
5937281340817,3
84509804,0
773054693,2
7log
593log
593log) 281340817,3
7 b
  2log100log7
2
100
log7
  893,11301,027 

12. Ejercicio.- Sabiendo el valor de log 2= 0,301030 y el de
log 3= 0,477121, calcula los siguientes logaritmos.
4loga).-
2
2log4log 
b).- 12log
12log
c).- 15log
 43log   2
23log  2
2log3log 
2log23log  079181,1301030,02477121,0 
602060,0301030,022log2 
15log
2
30
log
2
103
log

    2log10log3log
176091,1301030,01477121,0 

13. Ejercicio.- Calcula el valor de la siguiente expresión
a).-
35
6 2
2
5122
464
log


35
6 2
2
5122
464
log

  



  35
2
6 2
2 5122log464log
  








3
512log
2log
6
464log 25
2
2
2









3
512log
2log5
6
4log264log 2
2
22
3
19
6
38
6
4810
8
6
10
3
9
15
6
226












15. En este tema vamos a ver:
813 52
x
Ecuaciones Exponenciales
1502 1
x
Ecuaciones Logarítmicas
1log2log  x
Sistemas de Ecuaciones
 




4log
5loglog2
yx
yx

16. Ejercicio 6.-Resuelve
813 52
x

813 52
x
992
 xx
a).-
b).- 1502 1
x Aplicamos el concepto de logaritmo
150log1 2x
Como150 no es potencia entera de 2, para despejar x tenemos que
tener en cuenta la definición de logaritmo (propiedad VII)
2288,71x
45
33
2
x
452
 x 542
 x
3
3
2
1


x
x
2288,7
301029995,0
176091259,2
2log
150log

2288,612288,7  x

17. Ejercicio 7.-Resuelve
a).- 1log2log  x
1log2log  x
Aplicamos la propiedad III, logaritmo de un producto e igualamos
logaritmos y la propiedad II.
Es lógico que si dos logaritmos son iguales lo que hay dentro
tiene que ser igual ¡¡¡IMPORTANTE!!!
10log)2log(  x
10log)2log(  x
5
2
10
102  xx

18. b).- 23loglog 55 x
Aplicamos la propiedad IV, logaritmo de un cociente y aplicamos
la definición de logaritmo para transformar 2 en logaritmo.
2
555 5log25log
3
log 
x
Al igualar logaritmos, igualamos lo que contienen y por lo tanto:
75253255
3
2
 x
x

19. c).-   27log3log6 22  x
Aplicamos la propiedad V, logaritmo de una potencia e
igualamos.
  3
22
6
2 3log27log3log x
  36
33 x
2
126
12
614366
2
4
066
2
2









x
a
cabb
x
xx
  36933 22
 xxx
2
126
1

x
2
126
2

x

20. Ejercicio 8.-Resuelve el siguiente sistema de ecuaciones.
a).-





1loglog
22
yx
yx Aplicamos las propiedades como
en los casos anteriores.
1010loglog1loglog 
y
x
y
x
yx
Resolvemos el sistema
20202102
222112210
10
22







xxy
yyyy
yx
yx
Solución del sistema
20;2  xy

21. Ejercicio 9.-Resuelve el siguiente sistema de ecuaciones.
a).-
 




4log
5loglog2
yx
yx Aplicamos las propiedades como
en los casos anteriores.
5loglog2  yx
De la otra ecuación obtenemos
52
10logloglog  yx
  4log  yx
4
10 yx
Con lo que obtenemos un nuevo sistema que pasamos a resolver
52
10log100000logloglog  yx
5
2
5
2
1010loglog 
y
x
y
x
4
10log10000log)log(  yx
4
10log)log(  yx

22. 






4
5
2
10
10
yx
y
x
5
4
3
10
10

x
Resolvemos la y
Solución
x
y
4
10

5
4
3
5
4
2
10
10
10
10

x
x
x
33 993
101010  xx
10
10
10
10 3
4
3
 yx
10;103
 yx

23. Ejercicio 9.-Resuelve
1222 1
 xx
Hacemos que 2x = z y aplicando las propiedades de las potencias:
222 1
 xx
Llegamos a que:
22222 1
  xxxx
242  xz x
Resolvemos
123122  zzz
1222
  
zz
x
z
4
3
12
123  zz

24. Ejercicio 10.- Resuelve la ecuación.
     23log6log1log  xxx
Aplicamos la propiedad V, logaritmo de una potencia e
igualamos.
      23log61log  xxx
     2361  xxx
23652
 xxx 0822
 xx

25. 




2
62
2
362
x
Comprobamos que x=-4 no verifica la ecuación porque log(-5) no
existe. La solución es:
21 x
0822
 xx
 
12
81442
2
42






a
cabb
x
21 x
42 x

26. Busca enlaces a otras páginas relacionadas con el tema en…
www.juansanmartin.net