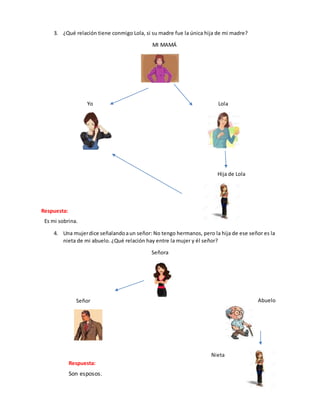
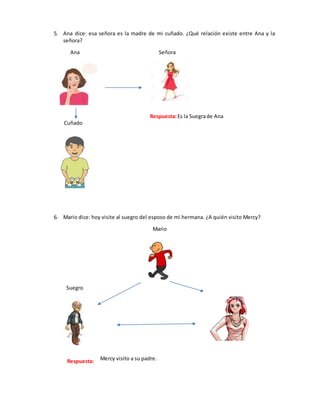
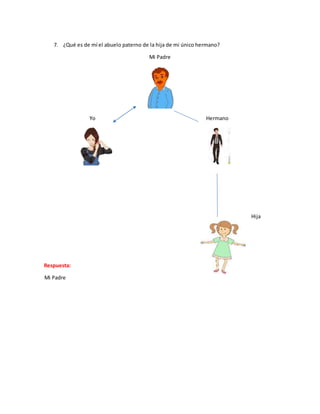
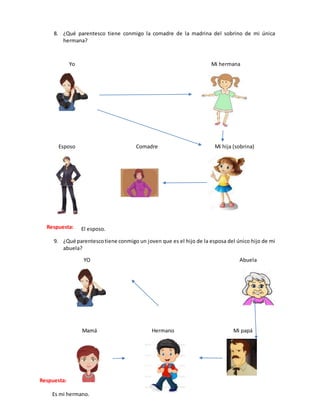
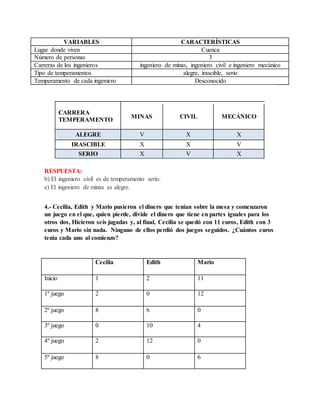
Este documento presenta una serie de ejercicios de resolución de problemas con una o dos variables. En la sesión 15, los ejercicios involucran problemas con una variable y se resuelven usando estrategias como dividir el todo en partes o identificar la diferencia entre cantidades. En la sesión 16, los ejercicios implican relaciones de orden como "más que" o "menos que". La sesión 17 presenta problemas de tablas y relaciones con dos variables.