Este documento analiza las funciones exponenciales y logarítmicas, explicando que la función exponencial tiene como dominio los números reales y su derivada es la misma función. Luego define las funciones exponenciales en base a y explica que son crecientes o decrecientes dependiendo del intervalo. Finalmente, explica las propiedades de los logaritmos, incluyendo que el logaritmo de un producto es la suma de los logaritmos de los factores y que los logaritmos naturales tienen como base el número e.

1. ANALICEMOS LA FUNCION
EXPONENCIAL Y LOGARÌTMICA

2. APLICAR CON SEGURIDAD LAS
FUNCIONES EXPONENCIALES Y
LOGARÍTMICAS AL UTILIZARLAS EN
LA RESOLUCION DE SITUACIONES
PROBLEMATICAS DEL ENTORNO
ESCOLAR Y SOCIAL

3. La función exponencial, es conocida formalmente como la función real ex,
donde e es el número de Euler, aproximadamente 2.71828...; esta función
tiene por dominio de definición el conjunto de los números reales, y tiene la
particularidad de que su derivada es la misma función. Se denota
equivalentemente como f(x)=ex o exp(x), donde e es la base de los logaritmos
naturales y corresponde a la función inversa del logaritmo natural.
En términos mucho más generales, una función real E(x) se dice que es
del tipo exponencial en base a si tiene la forma
Siendo a, K ∈ R números reales, con a > 0. Así pues, se obtiene un abanico
de exponenciales, todas ellas similares, que dependen de la base a que
utilicen.

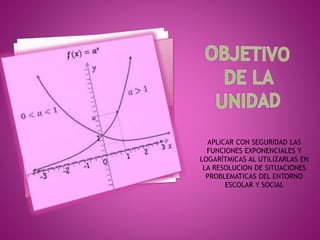
4. Una función es creciente en un intervalo [a,b] si al
tomar dos puntos cualesquiera del mismo, x1 y x2,
con la condición x1 £ x2, se verifica que
f( x1 ) < f( x2 ).
Se dice estrictamente creciente si de x1 < x2 se
deduce que f(x1) < f(x2).
Una función es decreciente en un intervalo [a,b] si
para cualesquiera puntos del intervalo, x1 y x2, que
cumplan x1 £ x2, entonces f(x1 ) ³ f(x2 ).
Siempre que de x1 < x2 se deduzca f(x1 ) > f(x2 ), la
función se dice estrictamente decreciente.

5. El sistema de numeración que
nosotros conocemos en la vida
cotidiana es el que tiene como
base 10 la función exponencial
de base 10 es f(x)= 10x

6. En matemáticas, el logaritmo de un número —en una base de logaritmo determinada— es
el exponente al cual hay que elevar la base para obtener dicho número. Por ejemplo, el logaritmo de
1000 en base 10 es 3, porque 1000 es igual a 10 a la potencia 3: 1000 = 103 = 10×10×10.
De la misma manera que la operación opuesta de la suma es la resta y la de la multiplicación la división,
el cálculo de logaritmos es la operación inversa a la exponenciación de la base del logaritmo.
Para representar la operación de logaritmo en una determinada base se escribe la abreviatura log y
como subíndice la base y después el número resultante del que deseamos hallar el logaritmo. Por
ejemplo, 35=243 luego log3243=5. Cuando se sobreentiende la base, se puede omitir.
Los logaritmos fueron introducidos por John Napier a principios del siglo XVII como un medio de
simplificación de los cálculos. Estos fueron prontamente adoptados por científicos, ingenieros,
banqueros y otros para realizar operaciones fácil y rápidamente, usando reglas de cálculo y tablas de
logaritmos. Estos dispositivos se basan en el hecho más importante — por identidades logarítmicas —
que el logaritmo de un producto es la suma de los logaritmos de los factores:

7. El logaritmo de 1=o
El logaritmo de base es igual a 1
El logaritmo de un producto es igual a la suma de logaritmo de cada uno
de los factores
El logaritmo de un cociente es igual al logaritmo del numerador menos el
logaritmo del denominador
El logaritmo de un potencia es igual producto del exponente por el
logaritmo de la base

8. Los logaritmo de base 10 se les
llama logaritmo comunes. cuando
se trabaja con logarítmo comunes
se omite el subíndice 10 que
indica cual es la base
en conclusión se tiene que:
El logaritmo común de 1 es
cero
El logaritmo común de un
numero mayor que 1 es
positivo
El logaritmo común de un
numero comprendido ente 0 y
1, es negativo

9. Los logaritmo cuya base es
el numero e, se
denominan logaritmos
natural
Propiedades de los
logaritmos naturales
El logaritmo natural de
1=0
El logaritmo natural de e
es igual a 1
El logaritmo natural de e
elevada al x es igual a x
e elevado a logaritmo
natural de x es igual a x